2019-04-01

LINE Fukuoka での 5 年間を振り返る

2019 年 5 月で LINE Fukuoka を退職します。

先日最終出社に成功して時間的に余裕ができたので、約 5 年間在籍した LINE Fukuoka の想い出を綴っていきたいと思います。退職は何度か経験していますが、ここまで感傷に浸れる会社は初めてです。長いようで短かった LINE Fukuoka で過ごした時間を振り返ることで、もう一度自分を見つめ直す良い機会になると信じて。感謝の気持ちを忘れないように。

エンジニアとしての僕

僕が LINE Fukuoka に来たのは 2014 年のこと。いわずもがな開発職としてジョインした。開発組織を立ち上げるという話が出てきたかなり初期の頃だったので、当時まだ福岡にはかなり少数のエンジニアしかいなくて、オフィスの端っこの空いたデスクに雑に座ってたのを思い出す。

最初の 3 年間は開発者としてほとんどの期間を LINE 占いやトーク占いというプロジェクトに費やし、その中で素晴らしく優秀でそれでいてとても優しい同僚と一緒に働くことができたのは、とても光栄だったし貴重な経験になった。ハッカソンやワークショップ、勉強会など、プロジェクト外の人たちと交流するたくさんの機会にも恵まれ、エンジニアとしても人間としても大きく成長できたと思う。

LINE Fukuoka は、これまで経験したことのない程の働きやすさで、エンジニアの働く環境については本当に文句のつけようがないくらい素晴らしかった。良い点を上げるとキリがないし、そういうのはインターネット上に割とたくさんころがってるけど、最も驚いたのは全員が全員、裁量労働制を使いこなしているということ。働かせ放題という空気は全くなく普通に午後から出社することも多かったし、僕なんかは 9 時前に出社して 18 時くらいには帰ってたし(もっと早く帰ることも多々あったし)、ほんとうに成果さえ出していれば自由に働ける環境だった。

それに、少なくとも僕のいた福岡ではエンジニア同士がお互いを信頼したり尊敬したりする文化が根付いていて、同僚も上司もみんな優しすぎた。本当に。たくさんの良い人達に恵まれて本当に幸せで、控えめに言って最高だと言える労働環境がそこにはあった。

とはいえ悪いところが 1 つもなかったのかと言うとそれはウソだし、巨大な組織ならではのやりにくさとか複雑性みたいなのはあったけど、愚痴や文句をインターネッツで書き殴るのはあまり好きではないので、気になる人は続きはオフラインで。

マネージャーとしての僕

そして、後半の 2 年間は機械学習やデータ分析を専門とする福岡の Data Labs という組織のマネージャーにロールチェンジして、組織の拡大や採用、メンバーのメンタリングなどに注力した。いま思い返すと福岡の Data Labs はたった 3 人で立ち上がった小さな小さなチームで当時はろくに期待もされてなかったと思うけど、福岡でバリューを発揮していくためにどうすればいいのかを必死に考えながら色々なことにチャレンジした結果、紆余曲折ありながらも今では福岡での役割や責任、認知度、組織の規模などが大きくなり、チームから室になるまでに成長することが出来たし、それにともなって室長という肩書もついた。

これはひとえにチームのみんなが一生懸命に頑張ってきたおかげとしか言いようがない。マネージャーはヒエラルキーの上層に位置するという見方をされるのが大半だけど、最近は単なるロールに過ぎないという考え方も多く、僕はその考えの方が好きだし実際にそう信じて役割を全うしてきた。

こうなるまでの道のりは当然平坦なものではなく、何度も壁にぶち当たっては現実逃避したり乗り越えようとしたりもがき苦しんできた。自分はこの会社に必要とされてるんだろうか、マネージャーなんていなくても組織はうまく回るのではないか、本当に福岡で Data Labs は必要とされているんだろうか、バリューは発揮できただろうか、ということは今でも不安になる。

組織の中での役割というのは自分の希望が単純に与えられるだけではなく、自分が動いた結果としてついてくることも多い。良くも悪くもほとんど全てのことは人によって決定されるし、会社という人格が存在するわけではない。そういう意味では会社それ自体は何も決めてくれないし、会社の方針もまたそこに属する人たちによって意思決定されている。マネジメント層に近づくにつれて誰も何も教えてくれずに、自分自身がその意思決定をしないといけなくなる。(当たり前のことだとは思うけれど) これが僕が室長になるまでの道のりで気付けたことであり、裁量と自由があるということは想像以上に辛く険しい道のりの途中に投げ出されるということ、いやそれは轍すら無いオフロードだとも言える。

ただしそれは悪いことではなく、自分の責任で何もない道を整備していくことができる - つまり “何でもできる” - ということにほかならない (決して職権の乱用とかそういう話ではない)。そういうところに気付いた上で、自分の手によって物事を良い方向に進めることができるんだと信じて正解の無い未来へ向けて行動してきたことこそが、先の自分の不安に対する自分なりの答えだったのかもしれない。

これからの僕

「せっかく室長にまでなったのに…」。辞めることを知った周囲の人たちが、一言目にはこう残念がることがあった。

LINE のような IT 企業に入ってエンジニアとして頑張ったあとに、マネジメント方向へ進みそのままシニアマネージャーとして活躍していくキャリアは、なるほどキラキラして見えるのだろう。僕としては、マネージャーが辛くなかったかというとそれはウソになるけど、楽しい面ももちろんあって、会社への貢献度を上げながら自分の組織が成長していく過程を体験するのはとてもやりがいはあったし面白かった。

だったんだけど、やっぱりどこかで捨て切れなかった。もう一度自分の手を動かし、物を作り出し、技術を追いかける、そういうエンジニアとしての生き方を。マネージャーへとキャリアチェンジする渦中、エンジニアとしての生き方を書き綴った 2017 年の振り返りの記事や、そこに書かれているエンジニアとしての行動原理などには、エンジニアを諦めきれない気持ちが見え隠れしている。もちろんマネージャーのとして役割を全うしようとこれまで頑張ってきたのは本当だし、一時期はずっとそのキャリアを歩んでいこうと考えたこともある。でも…ずっと違和感はあった。時が経つにつれてこの違和感の正体は自分でも分かるようになってきたけれど、それはこんなところでは書くことができない、まるでドロドロとしたようなものだ。

とにかく、僕はもう一度エンジニアとしてチャレンジしたいと願いながら会社と対話を続けてきたけれど、今回は思い切って外に飛び出してみることにした。LINE Fukuoka が嫌いなわけではない。LINE Fukuoka に入社してからは社内でも社外でも本当に数えきれない程たくさんの出会いがあって、その一つ一つがおしなべて僕の人生を豊かにしてくれた。一緒に働いてくれた同僚や上司には今となっては感謝の気持ちしか無い。わがままな話ではあるけど、もう少し、もう少しだけ僕の望むエンジニアとしての経験を積むことができたら、今度はマネジメントとしてのキャリアにも自信をもって飛び込めるんじゃないかなと思っている。もちろんそういう機会に恵まれれば、という話ではあるけど。

僕は今年で 35 歳になる。一昔前まではプログラマ 35 歳定年説という話をよく聞いたが、気付けばそれと同じ年齢にまで達してしまった。もちろん近年そんな話を信じてる人は少ないだろうし、まだまだ自分の能力を信じているので、これからも怖気づくことなく挑戦を続けたい。これまでの経験も引っさげて、ガムシャラに努力していこうと思う。

おわりに

さて、おわりに。

ここで書けないような楽しいことも辛いこともたくさんあったけど、それも全部含めて僕の LINE Fukuoka の 5 年間。先にも書いたけれど、LINE Fukuoka はエンジニアにとってとても働きやすい企業です。Data Labs も開発室も LINE Fukuoka それ自体も、まだまだ成長していけると信じていますしエンジニアの採用も積極的にやっているので、興味のある方は SNS でも実際に会った時でも、なんでもいいので私に声をかけてもらえれば社内の偉い人に繋ぐくらいはできそうです。(それが実際に採用に繋がるかどうかは別として笑)

最後に LINE Fukuoka の同僚や上司たちに向けて。さよならは悲しいので、またどこかで会えることを信じて…

いってきます！

2017-12-30

2017 年の振り返り

2017 年は自分にとってキャリアが大きく動いた年だった。

1 年を振り返る良い機会だし、ちょっと頭の中で考えていることをきちんと言葉にしてみようと思う。それってとても難しいことだから普段ほとんどすることはないけど、思考を言語化することは自分を見つめ直す良い機会になるはず。

エンジニアとしての生き方

プログラミングに初めて触れたのは遡ればもう高校入学時の夏。プログラミングってなんでこんなに楽しくて、こんなにも興味をそそるもので、僕を感動させてくれるんだろう、とすぐにプログラミングの虜になり、将来は絶対エンジニアになると誓っていた。それから約 15 年間、よくもまあ飽きもせず仕事でも趣味でもプログラミングを続けているものだと自分でも関心するけど、エンジニアってそういう生き物なのだ（ですよね？）。”楽しい” が僕にとっての行動原理だったりする。”生きるため” という考えの元では少しも長く続いていなかったろう。プログラミングが僕自身を輝かせ、道を作ってくれた。

そういう意味では、好きなことを仕事にすれば幸せになれるというのは誰もが考えるところだとは思うけど、そもそも好きなことを仕事にするのはかなり難しい。100% 好きなことだけをして働いて生きていくのは到底無理だし、好きなだけではどうにもならない。覚悟が必要だ。自分の働きによって、どれだけ世の中に貢献できるのか、いや世の中なんて大層なものではなくてもいいけれど、どれだけ周囲に貢献できるのか、その価値と常に向き合っていく必要がある。しかし、自分の価値の話をし始めると、どうしても自分以外にも目がいってしまう。特に僕達の業界では、その年齢でどこでいつのまにそれ程の知識を得たのか、時間の進み方が僕らとはちょっと違うのでは？と疑問を抱くほどの凄腕スターエンジニアがうようよいる。そんな人達には到底かなわないので、じゃあ自分なんて…と落ちてしまうこともある。

この辺のコントロールは本当に難しい。変化が速く激しいこの業界の中で自分の価値を見出し続けることは大変だし、人間なので落ちる時は落ちる。それを乗り越えられた時に、”楽しい” と “生きる” が繋がっていくのだと思う。要するに覚悟ってそういうことだ。自分を信じること。難しい問題も乗り越えられるように、いつでも自分を信じ続けること。

少し僕の話をすると、過去にプログラマのための数学勉強会@福岡を主催していた。僕は数学科卒業でも数学に関して秀でているわけでもないのでプログラマと数学という記事で「数学ができないなりの楽しさ」と題して悩みを書き殴っていたけど、当時は数学とプログラミングの “楽しい” を原動力に行動していた。加えて今年は幸運にも書籍の執筆もさせてもらって、その時の心境も「やさしく学ぶ機械学習を理解するための数学のきほん」を執筆しましたという記事にまとめおり、そこからもやはり悩みつつも、信じて行動し続けていたことがうかがえる。

これらは会社外での外向けの活動の話だけど、会社内での仕事の話だってそう変わらない。楽しいを原動力に、自分を信じてキャリアを積み上げていく。それが血となり肉となり、自分自身の価値となっていく。そうやって作っていった経験は誰にも真似出来ない自分だけの価値になっていく。

冒頭にも書いたけど、2017 年は自分にとって大きくキャリアが動いた節目の年だった。元来は Web や Android アプリケーションのエンジニアだった自分が、難しそうだったけど昔から好きだった機械学習やデータ分析を専門とした組織の立ち上げメンバーとして今年の頭から稼働してきた。それは、自分がそういった領域のエンジニアとしての価値を組織に対して提供できることを示してこれたからだと信じている。そして 2018 年からは、いわゆるマネージャーとしてのロールで組織にコミットしてく必要があり、いままでのように技術が好きなだけでは通用しない、組織の成長を俯瞰して見ていかなければならない。

だけど、自分のエンジニアとしての人生がそこで終わるわけではない。組織の中で与えられた役割は全うするべきだし、その役割の中で楽しいことはきっと見つけられる。それは好きなことを仕事にするってこととはちょっと違うかもしれないけど、これまで書いてきたエンジニアとして生きるための行動原理があったからこそいまの環境があると考えると、大きく外れた道ではなかったんだろうなと思うし、やっぱり好きだしそれを終わらせたくはない。個人的にプレイングマネージャーはあまり良くないと思うので、コードでコミットする時間は徐々に減っていくだろうけれど、プライベート含めゼロにはしたくないし、知識やスキルアップに関しては貪欲に求めていくように努力したい。

生き方や働き方、考え方なんて十人十色だし、これが正解という話はない。ただ、自分の中で信じることができる正解を持つことが、大事なんじゃないかな、って思う。

◎◎◎

振り返り

まとまりのない感じになったんで、2017 年の印象的な出来事を軽く振り返ってみます。

データ分析組織

いまの勤め先で新しくデータ分析専門の組織が立ち上がり、初期メンバーとして稼働しました。立ち上げ自体は昨年ですが、実稼働し始めたのはだいたい今年頭からです。

[エンジニア対談]LINE Fukuokaのデータ分析・機械学習エンジニアとして取り組んでいきたいこととは？

もちろん私自身が立ち上げたわけではありませんが、以前から福岡にもそういう組織があるといいのでは、と声を上げていたのは事実でした。データ分析専門とはいいつつも、いわゆるデータサイエンティストと呼ばれる分析屋だけではなく、データ分析のためのインフラを管理したり機械学習によるテキスト分類など割りとエンジニアリング寄りなタスクもこなす集団になっていると思います。

英語環境

2017 年は特に英語を使う機会がとにかく多い一年でした。いまの会社はとにかくグローバル感が半端ないです。

【社員インタビュー】技術好奇心×カルチャー開発室室長が語るLINE Fukuokaの開発組織

この記事で室長が言っているようにいまの開発室は半数以上が外国籍社員です。これはデータ分析のチームも例外ではなく、そうなると必然的に英語によるコミュニケーションも増えてきます。もともと英語は嫌いな教科ではなかったけど、Reading / Writing だけじゃなくてまさか Listening / Speaking まで出来るようになるとは思ってもいない成長でした。(とはいえまだまだ Broken な英語ではあるので、もっと慣れが必要)

書籍執筆

幸運なことにマイナビ出版から書籍を出版させていただきました。

やさしく学ぶ機械学習を理解するための数学のきほん

書籍の内容や出版の経緯などはこの記事にまとめている。おかげさまで何度か重版され、身近なエンジニア数人も買ってくれていて嬉しい限り。

PHPカンファレンス福岡2017

いまではもう PHP 書かないけど…。Fukuoka.php コミュニティと、この PHP カンファレンス福岡は昔からファンだったので、その大舞台で登壇できたというのは非常に良い思い出になりました。名の知れた有名なエンジニアの方もたくさんいらっしゃっていて、当時から憧れていた人も多かったので、そのような方々と同じ場でしゃべることができたというのは本当に嬉しかったです。

子どもたちの成長

上の子が小学校、下の子が幼稚園にそれぞれ通い始めました。毎日ケンカしてストレス溜まるけど、毎日何かしら笑顔をくれるので、ん〜、まあ相殺？

2017-09-06

「やさしく学ぶ機械学習を理解するための数学のきほん」を執筆しました

私が執筆した書籍やさしく学ぶ機械学習を理解するための数学のきほんがマイナビ出版から Amazon で 2017/9/20 より発売されます。Amazon 上では既に予約可能になっていますので、興味のある方は是非とも手に取ってみてください。

本書は、以前よりこのブログ内で公開していた「やる夫で学ぶ機械学習シリーズ」というシリーズ物の記事をベースとして、加筆・修正を加えたものになります。ブログの記事がベースになってはいますが、追加で書いた分の方が多く、お金を出して買ってもらえるクオリティにするために、より丁寧な説明を心がけて書きました。元記事は「やる夫」と「やらない夫」というキャラクターを登場人物として、機械学習の基礎を面白おかしく丁寧に解説していくものでしたが、書籍化するに当たって「やる夫」と「やらない夫」をそのまま使うわけにもいかなかったので、プログラマの「アヤノ」とその友達で機械学習に詳しい「ミオ」というキャラクターを新しく作って、彼女らの会話を通して一緒に勉強していく形を取っています。この本は以下のような構成になっていて、Chapter 1 〜 5 が本編で、Appendix で必要な数学知識の補足をしています。

Chapter 1 - ふたりの旅の始まり
Chapter 2 - 回帰について学ぼう
Chapter 3 - 分類について学ぼう
Chapter 4 - 評価してみよう
Chapter 5 - 実装してみよう
Appendix (本編に入り切らなかった数学知識の解説)

会話形式なので、全体的な文量もそこまで多くなくスラスラ読んでいけると思います。ただし、本書は機械学習の数学に関する入門書という位置付けなので、プログラミング自体の入門解説だったり、いろいろなアルゴリズムの紹介だったりは、内容にありません。Chapter 2 及び Chapter 3 あたりが、いま公開されているブログ記事ベースになっていますので、いきなり本を買うのが嫌な方や試し読みをしてみたい方などは、まずやる夫で学ぶ機械学習シリーズを読んでみると、感覚をつかんでいただけるのではないかなと思います。また、マイナビ出版の Facebook には本書のサンプルページが掲載されていますので、そちらを見ても雰囲気はつかんでいただけるかなと思います。

執筆にかけた想い

書籍の宣伝はこの辺にして、ここからは個人的な想いを書いたポエムですので、ご了承ください。

- 数学や機械学習を通じて、気軽に話したりお互いに刺激し合える仲間が欲しい -

始まりは、ただ、それだけでした。

私がいわゆる機械学習と言われる領域に足を踏み入れた頃は、いまほど界隈は賑わっていませんでした。元々は大学時代からコンピュータービジョンや 3D に興味があり、それらに関するアルゴリズムや実装を探しているうちに機械学習に興味をもって勉強し始めましたが、もちろん当時は参考にできる Web サイトも書籍も、今よりも少ない状態です。仕事として機械学習をやっているわけでもなく、手取り足取り教えてくれるような詳しい人や、機械学習に興味を持っていそうな人は周りにはおらず、毎日ひとりでアテもなく先の見えない道を進むばかりだったのを覚えています。一人きりで何かを続けていくことほど、モチベーションが長続きしないことはありません。

そんな状況でしたのでちょっとだけ勉強には苦労していたのですが、学生時代から数学が好きだったこともあり (得意かどうかは置いといて) 数学に対する抵抗はまったくありませんでした。むしろ数学をやっている時間は一人でも楽しくて、没頭することができました。そうして勉強しながらしばらく時が経ち、世の中が機械学習やディープラーニングで盛り上がりを見せ始めたのをきっかけに、自分のブログでもぽつぽつと機械学習に関する情報を発信するようになっていきます。また、数学好きが高じてプログラマのための数学勉強会@福岡というイベントも主催していました。そうやってアウトプットを続けていれば、きっと仲間が集って、いつかみんなでワイワイできるようになるんだ、と信じて。

そういったアウトプットの一環としてやる夫で学ぶ機械学習シリーズは産まれました。このシリーズは「わかるって楽しい」をコンセプトに、なるべく読者を置いてけぼりにしないように気をつけながら書いていました。シリーズ目次には「まとめることで知識を体系化できて自分の為になる」などと書いてますが、先にも仲間集めをしたいと言っていたように、本当は もっと身近に機械学習に興味がある人や仲間を増やしたい という理由がありました。自分なんかが書いた記事で機械学習に興味を持ってくれる人が増えると考えるなんておこがましい、と割りとネガティブに考えていて、無理やり別の理由をくっつけていたのですが、幸運なことに公開後に非常に大きな反響をいただきました。そのおかげで「あのブログ読みました」と声をかけていただくことも多くなりましたし、結果的にこのシリーズをベースに書籍の執筆の機会をいただくことが出来ました。このシリーズ記事を通じて、機械学習の基礎を理解して興味を持ってくれた人がいたとすると非常に嬉しいですし、そういう人が増えてくれると記事を書いた甲斐があったというものです。

そして、私のその想いは書籍になっても変わりません。いまは時代も移り変わり、初心者向けの解説書や Web の記事はたくさんあり、導入の敷居は確実に当時よりも下がっています。そんな中、あえて本書を選んで手にとってくれた方には是非とも、一緒に話したり勉強したりできる仲間を作って、そして私のようにひとりぼっちで悩むことがないように情報を発信し続けてくれればいいな、と思っています。

願わくば一人でも多くの機械学習へ興味を持つ方へ本書が届き、そして役に立ってくれますように。

2016-08-22

機械学習でパラメータ推定 - 最尤推定法 -

最尤推定法 (Maximum Likelyhood や Maximum Likelyhood Estimation と言われ、それぞれ頭文字を取って ML や MLE などとも言われる) は機械学習やコンピュータービジョンなどの分野で良く使われる推定法で、次のような条件付き同時確率を最大化することでパラメータの推定を行います。

$\hat{\theta} = \mathop{\mathrm{argmax}}\limits_{\theta} \mathrm{P}(x_1, x_2, \cdots, x_N|\theta)$

これだけ見て「うん、アレね」と理解できる人はこの記事の対象読者ではなさそうですので、逆にいろいろ教えて下さい。この記事では理論の面から最尤推定法にアタックしてみます。数式成分が多めで、うっとなることもあるかもしれませんが、ゆっくり読んでいきましょう。

※この記事を読むにあたっては、確率論と微分の基礎知識程度は必要です。

尤度

いきなり応用問題から始めると必ず挫折するので、まずは一番簡単な問題設定から始めます。Wikipedia に最尤推定のページがありますので、この中で使われている例を参考に話を進めていきましょう。

見た目がまったく同じ 3 枚のコイン A, B, C があります。これらのコインはイカサマで、投げた時に表の出る確率がそれぞれ違います。

コイン A は ¹⁄₃ の確率で表が出る
コイン B は ¹⁄₂ の確率で表が出る
コイン C は ²⁄₃ の確率で表が出る

この 3 枚のコインを箱の中に入れてシャッフルした後に 1 枚引きます。引いたコインを 10 回投げたら、表が 3 回、裏が 7 回出ました。あなたは A, B, C のどのコインを引いたでしょうか？

この問題設定は極めて単純です。単純すぎて最尤推定法を使わなくても解けるくらい簡単ですが、ここでは敢えて最尤推定法を使って解いてみます。最尤推定法は次の条件付き同時確率を最大化するパラメータ $\hat{\theta}$ を求めることでした。

$\hat{\theta} = \mathop{\mathrm{argmax}}\limits_{\theta} \mathrm{P}(x_1, x_2, \cdots, x_N|\ \theta)$

$x_1$ は 1 回目に投げた時の結果、 $x_2$ は 2 回目に投げた時の結果、 $x_N$ は N 回目に投げた時の結果になります。コインは全部で 10 回投げることになっているので $N=10$ なのは自明ですよね？これらは、統計学や機械学習の文脈では観測データや学習データとも言われますが、先の問題設定では表が 3 回、裏が 7 回出たということなので、例えばですがこんな風に表せます。(表、裏、みたいな単語だと扱いにくいので、今後は表 = 1、裏 = 0 という風に数値に変換して扱います)

$x_1 = 0$ (裏)
$x_2 = 1$ (表)
$x_3 = 0$ (裏)
$x_4 = 0$ (裏)
$x_5 = 0$ (裏)
$x_6 = 0$ (裏)
$x_7 = 1$ (表)
$x_8 = 1$ (表)
$x_9 = 0$ (裏)
$x_{10} = 0$ (裏)

ここでちょっとコイントスについて考えます。問題ではコインを 10 回投げていますが、それぞれのコイントスは独立だと考えます。要するに 1 回目に表か裏かどちらが出ようが、2 回目のトスには何の影響も与えないと考えます (3 回目以降も同様) 。まあ普通そうですよね。各試行が独立だと考えると、同時確率は各試行の確率の積に分解できるので、こう書き換えることができます。

$\mathrm{P}(x_1, x_2, \cdots, x_{10}|\ \theta) = \prod_i^{10} \mathrm{P}(x_i|\ \theta)$

じゃあ $\mathrm{P}$ と $\theta$ は何かというと、確率分布とそのパラメータです。確率分布はそれぞれ固有のパラメータを持っていて、そのパラメータが決まれば分布の形が決まります。たとえば…

正規分布: 平均 $\mu$ と分散 $\sigma^2$ という 2 つのパラメータを持つ
t分布: 自由度 $\nu$ というパラメータを持つ
ベルヌーイ分布: $\lambda$ というパラメータを持つ

式中ではパラメータのことを $\theta$ と書いてはいますが、これを見てわかるようにパラメータは確率分布によって全然違うのでそれを何か 1 つの文字にまとめているというだけで、確率分布によって様々に変わります。

ここでは箱から引いたコインを投げた時にどれくらいの確率で表が出るのか、ということを知りたいので、確率 $\lambda$ で 1 が出て、確率 $1 - \lambda$ で 0 が出る、というベルヌーイ分布を考えます。たとえば $\lambda = 0.4$ だとすると、40% の確率で 1 が、60% の確率で 0 が出ることになります。ベルヌーイ分布はこのように数式で表すことができます。

$\mathrm{P}(x\ |\ \lambda) = \lambda^x (1-\lambda)^{1-x} \ \ \ \ (0 \le \lambda \le 1,\ \ x \in \{0,1\})$

これを最尤推定法の式に代入すると最終的にはこう書くことができます。

$\begin{eqnarray} \mathrm{P}(x_1, x_2, \cdots, x_{10}|\ \theta) & = & \prod_i^{10} \mathrm{P}(x_i|\ \theta) \ & = & \prod_i^{10} \lambda^{x_i} (1-\lambda)^{1-x_i} \end{eqnarray}$

この式がどういうことを意味しているのかをちょっと考えてみます。この式は尤度と呼ばれており、パラメータ $\lambda$ が与えられた時に、その $\lambda$ がどれくらい学習データを尤もらしく説明できているかという指標になります。尤度という概念はとてもわかりづらく、言葉だけでは少し理解しにくいので、実際に値を計算してみましょう。たとえば $\lambda$ を適当に 3 つ決めて、それぞれの $\lambda$ で式の値を求めてみます。

$\lambda = 0.05$ (5% の確率で表が出るコイン) の場合

$\begin{eqnarray} \prod_i^{10} 0.05^{x_i} (1-0.05)^{1-x_i} & = & 0.95 \cdot 0.05 \cdot 0.95 \cdot 0.95 \cdot 0.95 \cdot 0.95 \cdot 0.05 \cdot 0.05 \cdot 0.95 \cdot 0.95 \ & = & 0.00008729216 \end{eqnarray}$

$\lambda = 0.33$ (33% の確率で表が出るコイン) の場合

$\begin{eqnarray} \prod_i^{10} 0.33^{x_i} (1-0.33)^{1-x_i} & = & 0.67 \cdot 0.33 \cdot 0.67 \cdot 0.67 \cdot 0.67 \cdot 0.67 \cdot 0.33 \cdot 0.33 \cdot 0.67 \cdot 0.67 \ & = & 0.00217803792 \end{eqnarray}$

$\lambda = 0.91$ (91% の確率で表が出るコイン) の場合

$\begin{eqnarray} \prod_i^{10} 0.91^{x_i} (1-0.91)^{1-x_i} & = & 0.09 \cdot 0.91 \cdot 0.09 \cdot 0.09 \cdot 0.09 \cdot 0.09 \cdot 0.91 \cdot 0.91 \cdot 0.09 \cdot 0.09 \ & = & 0.00000003604 \end{eqnarray}$

これは、最初に学習データとして得られた $x_1, x_2, \cdots, x_{10}$ が どういうコインから生成されたものか という指標をしめしています。10 回中 3 回だけ表が出るという結果が、 $\lambda = 0.91$ のコインから生成されることは稀でしょう。 $\lambda = 0.91$ ということは表が出る確率が 91% もあるので、3 回とは言わずもっと表が出るはずです。逆に $\lambda = 0.05$ の場合は、表が出る確率は 5% ということなので、10 回中 3 回も表が出ているという結果はあまり納得のいく結果ではありません。結局は $\lambda = 0.33$ というコインが、一番うまく結果を説明しています。

これは、尤度の値を見てみれば一目瞭然です。3 つの尤度を比べてみると $\lambda = 0.33$ の尤度が最も大きく、続いて $\lambda = 0.05$ 、そして $\lambda = 0.91$ が最も小さくなっています。要するに尤度の値が大きければ大きいほど、うまくデータを説明してくれる尤もらしいパラメータであると言えます。

この辺りまで理解できるとゴールが見えてきます。最初に示した最尤推定法の式を覚えていますか？これは今考えているコインの問題に対しては、最終的にこのように変形できます。

$\begin{eqnarray} \hat{\theta} & = & \mathop{\mathrm{argmax}}\limits_{\theta} \mathrm{P}(x_1, x_2, \cdots, x_{10}|\ \theta) \ & = & \mathop{\mathrm{argmax}}\limits_{\theta} \prod_i^{10} \mathrm{P}(x_i|\ \theta) \ & = & \mathop{\mathrm{argmax}}\limits_{\lambda} \prod_i^{10} \lambda^{x_i} (1-\lambda)^{1-x_i} \end{eqnarray}$

これは尤度を最大にする $\lambda$ を求める、という意味の式です。尤度が最大になる $\lambda$ がわかれば、観測された学習データ $x_1, x_2, \cdots, x_{10}$ がどういうコインを使って生成されたものなのか、言い換えればどういうコインを投げると $x_1, x_2, \cdots, x_{10}$ という結果が出てくるのか、ということがわかります。

尤度を最大化するパラメータを推定する、これが最尤推定です。

最適化問題

尤度を最大化するという最適化問題なので、あとは最適化問題を解くためのアルゴリズムに従って解いていくだけです。ここでは最大化したい尤度を $L$ として、このように表します。

$L(\lambda) = \prod_i^{10} \lambda^{x_i} (1-\lambda)^{1-x_i}$

ただし、一般的にはこの $L$ をそのまま最大化するのではなく尤度の対数を取った対数尤度 $\log L$ を最大化します。

$\begin{eqnarray} \log L(\lambda) & = & \log \prod_i^{10} \lambda^{x_i} (1-\lambda)^{1-x_i} \ & = & \sum_i^{10} \log \lambda^{x_i} (1-\lambda)^{1-x_i} \ & = & \sum_i^{10} \left( x_i \log \lambda + (1 - x_i) \log (1 - \lambda) \right) \end{eqnarray}$

対数を取る理由は主には、計算を簡単にするためとアンダーフローを防ぐためです。今計算しようとしている尤度は要するに同時確率なので確率の積になっていますが、対数を取ると積を和に変換できます。また、さっき具体的にパラメータを代入して尤度を計算してみてわかったと思いますが、同時確率の計算は値が急激に小さくなっていきます。これも対数を取ることで積が和に変換されるので、値が小さくなることを防げます。

さて、この $\log L(\lambda)$ が最大になるような $\lambda$ を探すことが目的でした。関数の最大値を探す時は微分した結果を = 0 と置いて、微分した変数について解けばよいですよね (関数が単純な凸関数である場合に限られますが) 。

$\begin{eqnarray} \frac{d \log L(\lambda)}{d \lambda} & = & \sum_i^{10} ( \frac{x_i}{\lambda} - \frac{1 - x_i}{1 - \lambda}) \ & = & \frac{1}{\lambda(1 - \lambda)} \sum_i^{10} (x_i - \lambda) \end{eqnarray}$

微分結果が求まったので、これを = 0 と置いて $\lambda$ について解きます。

$\begin{eqnarray} \frac{1}{\lambda(1 - \lambda)} \sum_i^{10} (x_i - \lambda) & = & 0 \ \sum_i^{10} x_i - 10 \lambda & = & 0 \ \lambda & = & \frac{1}{10} \sum_i^{10} x_i \end{eqnarray}$

これで答えがでました。このような式で求めた $\lambda$ が尤度を最大にします。実際に $x_1, x_2, \cdots, x_{10}$ を代入して計算してみると

$\begin{eqnarray} \lambda & = & \frac{1}{10} \sum_i^{10} x_i \ & = & \frac{1}{10} (0 + 1 + 0 + 0 + 0 + 0 + 1 + 1 + 0 + 0) \ & = & \frac{3}{10} \end{eqnarray}$

これは ³⁄₁₀ の確率で表が出るコインであれば尤度が最大になるということで、これに一番近いコインは A になり (A は ¹⁄₃ の確率で表が出るコイン)、観測された学習データから考えるとあなたが引いたコインは A だろうということが言えます。

気付いた人もいるかもしれませんが、10 回中 3 回表が出るんだったら、そりゃあ ³⁄₁₀ になるのは直感的に当然だろうって思いますよね。これは問題設定が単純ってこともあるかもしれませんが、 $x_1, x_2, \cdots, x_{10}$ というデータだけから判断した結果なのでそうなるのも分かる気がしますね。

正規分布のパラメータ推定

最後に正規分布についても例を見て終わりたいと思います。

ベルヌーイ分布のパラメータは $\lambda$ ひとつだけでしたが、正規分布は平均 $\mu$ と分散 $\sigma^2$ の 2 つのパラメータを持っていますので、尤度を最大化するためにそれぞれ $\mu$ と $\sigma^2$ をそれぞれ求めます。今回は確率分布 $\mathrm{P}$ に正規分布を使うので尤度はこうなります。

$\begin{eqnarray} L & = & \mathrm{P}(x_1, x_2, \cdots, x_N|\ \theta) \ & = & \prod_i^N \mathrm{P}(x_i|\ \theta) \ & = & \prod_i^N \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2} \right) \end{eqnarray}$

同じようにこの尤度を $L$ として対数を取ると、このように変形できます。

$\begin{eqnarray} \log L & = & \log \prod_i^N \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2} \right) \ & = & \sum_i^N \log \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2} \right) \ & = & \sum_i^N \left( -\log \sqrt{2 \pi} -\frac{1}{2}\log \sigma^2 - \frac{(x_i - \mu)^2}{2\sigma^2} \right) \end{eqnarray}$

ベルヌーイ分布を考えた時と同様に、この対数尤度関数を $\mu$ と $\sigma^2$ について微分して、それぞれ = 0 と置いて解いていきます。正規分布ではパラメータが 2 つある多変数関数なので偏微分になります。

まずは $\mu$ で偏微分をするところから。

$\begin{eqnarray} \frac{\partial \log L}{\partial \mu} & = & \sum_i^N \left(0 + 0 + \frac{(x_i - \mu)}{\sigma^2} \right) \ & = & \frac{1}{\sigma^2} \sum_i^N (x_i - \mu) \end{eqnarray}$

これを = 0 と置いて $\mu$ について解いていきます。

$\begin{eqnarray} \frac{1}{\sigma^2} \sum_i^N (x_i - \mu) & = & 0 \ \sum_i^N x_i - N\mu & = & 0 \ \mu & = & \frac{1}{N} \sum_i^N x_i \end{eqnarray}$

これでまずは尤度を最大にする $\mu$ が見つかりました。次は $\sigma^2$ について解いていきます。まずは偏微分から。

$\begin{eqnarray} \frac{\partial \log L}{\partial \sigma^2} & = & \sum_i^N \left(0 - \frac{1}{2\sigma^2} + \frac{(x_i - \mu)^2}{2\sigma^4} \right) \ & = & -\frac{N}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_i^{N}(x_i-\mu)^2 \end{eqnarray}$

同じようにこれを = 0 と置いて $\sigma^2$ について解きます。

$\begin{eqnarray} -\frac{N}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_i^{N}(x_i-\mu)^2 & = & 0 \ -N\sigma^2 + \sum_i^{N}(x_i-\mu)^2 & = & 0 \ \sigma^2 & = & \frac{1}{N}\sum_i^{N}(x_i-\mu)^2 \end{eqnarray}$

これで尤度を最大にする正規分布のパラメータ $\mu$ と $\sigma^2$ がわかりました。

$\begin{eqnarray} \mu & = & \frac{1}{N} \sum_i^N x_i \ \sigma^2 & = & \frac{1}{N}\sum_i^{N}(x_i-\mu)^2 \end{eqnarray}$

これは純粋なデータの平均と分散になっています。

まとめ

尤度を最大化してパラメータを推定するための最尤推定法を紹介してきました。学習データからモデルのパラメータ $\theta$ を訓練することが目的ではなく、最終的にやりたいことは新しい未知データがどれだけモデルに適合しているのか推論することです。最尤推定は比較的簡単な手法だと思うので、試しに実装してみると面白いと思います。

2016-06-16

やる夫で学ぶ機械学習 - 対数尤度関数 -

やる夫で学ぶ機械学習シリーズの第 6 回です。ロジスティック回帰の目的関数である尤度関数をもう少し詳しくみて、線形分離不可能な問題にどのように適用していくのかを見ていきます。

第 5 回はこちら。やる夫で学ぶ機械学習 - ロジスティック回帰 -

目次はこちら。やる夫で学ぶ機械学習シリーズ

対数尤度関数

やらない夫
尤度関数を微分してパラメータ $\boldsymbol{\theta}$ の更新式を求めてみようか。

やる夫
もう脳みそパンパンですお。

やらない夫
その前に、尤度関数はそのままだと扱いにくいから、少し変形しよう。

やる夫
扱いにくい？どういうことかお？

やらない夫
まず同時確率という点だ。確率なので 1 以下の数の掛け算の連続になることはわかるな？

やる夫
確かに、確率の値としては 0 より大きくて 1 より小さいものだお。

やらない夫
1 より小さい数を何度も掛け算すると、どんどん値が小さくなっていくだろう。コンピュータで計算する場合はそれは致命的な問題だ。

やる夫
あー、オーバーフローの逆かお。アンダーフロー。

やらない夫
次に掛け算という点だ。掛け算は足し算に比べて計算が面倒だ。

やる夫
小数点の計算とかあんまりやりたくないお。

やらない夫
そこで一般的には尤度関数の対数をとったもの、対数尤度関数を使う。

$\log L(\boldsymbol{\theta}) = \log \prod_{i=1}^n P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}}$

やる夫
目的関数に対して勝手に対数をとったりして、答え変わらないのかお？

やらない夫
問題ない。対数関数は単調増加な関数だからだ。対数関数のグラフの形を覚えているか？

やる夫
確かこんな感じのグラフだお。

やらない夫
それで正解だ。グラフがずっと右上がりになってることがわかるだろう。つまり単調増加な関数ってのは $x_1 < x_2$ ならば $f(x_1) < f(x_2)$ となるような関数 $f(x)$ だということだ。

やる夫
なるほど、確かに $\log(x)$ はそういう風になっているお。

やらない夫
$\log$ は単調増加関数だから、今考えいてる対数尤度関数についても $L(\boldsymbol{\theta_1}) < L(\boldsymbol{\theta_2})$ であれば $\log L(\boldsymbol{\theta_1}) < \log L(\boldsymbol{\theta_2})$ ということが言えるだろう。要するに $L(\boldsymbol{\theta})$ を最大化することと $\log L(\boldsymbol{\theta})$ を最大化することは同じことなんだ。

やる夫
ふーん、よく考えられてるお。

やらない夫
では、対数尤度関数を少し変形して $f_{\boldsymbol{\theta}}$ を使って表してみよう。

$\begin{eqnarray} \log L(\boldsymbol{\theta}) & = & \log \prod_{i=1}^n P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}} \ & = & \sum_{i=1}^n \left( \log P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} + \log P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}} \right) \ & = & \sum_{i=1}^n \left( y^{(i)} \log P(y^{(i)}=1|\boldsymbol{x}) + (1-y^{(i)}) \log P(y^{(i)}=0|\boldsymbol{x}) \right) \ & = & \sum_{i=1}^n \left( y^{(i)} \log f_{\boldsymbol{\theta}}(\boldsymbol{x}) + (1-y^{(i)}) \log (1-f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) \end{eqnarray}$

やる夫
うっ、ちょっと式変形を追うのが大変だお…

やらない夫
実際には 2 行目は $\log(ab) = \log a + \log b$ という性質を、3 行目は $\log a^b = b \log a$ という性質を使っているだけだ。

やる夫
$\log$ の性質は覚えてるけど、最後の行はなんでそうなるんだお。

やらない夫
確率の定義からだ。ここでは確率変数の取る値としては $y=1$ か $y=0$ かしかないから、 $P(y^{(i)}=1|\boldsymbol{x}) = f_{\boldsymbol{\theta}}(\boldsymbol{x})$ ならば $P(y^{(i)}=0|\boldsymbol{x}) = 1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})$ となる。

やる夫
あー、そうか。全部の確率を足すと 1 になるんだったお。

やらない夫
ここまでで俺たちは目的関数として対数尤度関数 $\log L(\boldsymbol{\theta})$ を定義した。次はどうする？

やる夫
$\log L(\boldsymbol{\theta})$ を $\boldsymbol{\theta}$ の各要素 $\theta_j$ で微分…かお？

やらない夫
ではこれを微分していこう。

$\frac{\partial}{\partial \theta_j} \sum_{i=1}^n \left( y^{(i)} \log f_{\boldsymbol{\theta}}(\boldsymbol{x}) + (1-y^{(i)}) \log (1-f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right)$

やる夫
ちょっと何言ってるかよくわからん式だお…

やらない夫
回帰の時にやったように、合成関数の微分を使うんだ。

やる夫
えーと、要するに…こうかお？

$\frac{\partial \log L(\boldsymbol{\theta})}{\partial f_{\boldsymbol{\theta}}} \cdot \frac{\partial f_{\boldsymbol{\theta}}}{\partial \theta_j}$

やらない夫
それでいい。ひとつずつ微分していくんだ。まず第一項はどうなるだろう？

やる夫
第一項は $\log L(\boldsymbol{\theta})$ を $f_{\boldsymbol{\theta}}$ で微分するんだから…えーっと、 $\log(x)$ の微分は $\frac{1}{x}$ でよかったかお？

$\begin{eqnarray} \frac{\partial \log L(\boldsymbol{\theta})}{\partial f_{\boldsymbol{\theta}}} & = & \frac{\partial}{\partial f_{\boldsymbol{\theta}}}\sum_{i=1}^n \left( y^{(i)} \log f_{\boldsymbol{\theta}}(\boldsymbol{x}) + (1-y^{(i)}) \log (1-f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) \ & = & \sum_{i=1}^n \left( \frac{y^{(i)}}{f_{\boldsymbol{\theta}}(\boldsymbol{x})} - \frac{1-y^{(i)}}{1-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \right) \ \end{eqnarray}$

やる夫
一気に第二項もやってしまうお。これも合成関数の微分を使うお。 $z = 1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})$ と置いて $f_{\boldsymbol{\theta}}(\boldsymbol{x}) = z^{-1}$ とすると

$\begin{eqnarray} \frac{\partial f_{\boldsymbol{\theta}}}{\partial \theta_j} & = & \frac{\partial f_{\boldsymbol{\theta}}}{\partial z} \cdot \frac{\partial z}{\partial \theta_j} \ & = & -\frac{1}{z^2} \cdot -x_j \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x}) \ & = & \frac{x_j \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{(1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}))^2} \end{eqnarray}$

やる夫
できたお！これが微分結果だお。

$\frac{\partial \log L(\boldsymbol{\theta})}{\partial \theta_j} = \sum_{i=1}^n \left( \frac{y^{(i)}}{f_{\boldsymbol{\theta}}(\boldsymbol{x})} - \frac{1-y^{(i)}}{1-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \right) \frac{x_j \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{(1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}))^2}$

やらない夫
そうだ、と言いたいところだが、ただ計算すればいいってもんじゃないだろ…やる夫はこれを見てどう思う？

やる夫
どう思うも何も、これでパラメータの更新式ができるお…まあ、二度と見たくもないような複雑な式ですお。

やらない夫
そう、実はまだ複雑なんだ。もう少し式変形を進めて綺麗な形にできるんだが…

やる夫
やる夫の計算力が足りないってことかお！

やらない夫
いや、ここまでできただけでも十分だ。一緒に考えよう。まず、後ろの方の $\exp$ が含まれている式の方を見てみようか。やる夫は全部まとめているが、そこをあえてこんな風に分けてみよう。

$\frac{x_j \exp(\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{(1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}))^2} = \frac{1}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot \frac{\exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot x_j$

やる夫
えっ、わざわざ分解するのかお。

やらない夫
そうするとこういう風に $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ を使って書けるだろう。

$\frac{1}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot \frac{\exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot x_j = f_{\boldsymbol{\theta}}(\boldsymbol{x}) \cdot (1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})) \cdot x_j$

やる夫
あーなるほど。確かにやらない夫の言う通りに変形できそうだお。でも、第二項が $1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})$ になるのはわかるけど、そんなの気付けないお…

やらない夫
式を変形する作業は慣れの問題も大きいだろうから、できなかったといってヘコむことはない。ちなみにシグモイド関数、ここでは $\sigma(x)$ と置こう、これの微分が $\sigma(x)(1-\sigma(x))$ になるのは有名だな。

やる夫
確かに $f_{\boldsymbol{\theta}}$ はシグモイド関数で、それを微分した形はそうなってるお。

やらない夫
では、この式を微分結果に代入してみよう。約分した後に展開して整理すると最終的にはこんな形になる。

$\begin{eqnarray} \frac{\partial \log L(\boldsymbol{\theta})}{\partial \theta_j} & = & \sum_{i=1}^n \left( \frac{y^{(i)}}{f_{\boldsymbol{\theta}}(\boldsymbol{x})} - \frac{1-y^{(i)}}{1-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \right) f_{\boldsymbol{\theta}}(\boldsymbol{x}) (1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})) x_j \ & = & \sum_{i=1}^n \left( y^{(i)}(1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})) - (1-y^{(i)})f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) x_j \ & = & \sum_{i=1}^n \left(y^{(i)} - f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) x_j \end{eqnarray}$

やる夫
めちゃくちゃ単純な式になったお…やらない夫すごすぎるお。

やらない夫
あとはいつものように、この式からパラメータ更新式を導出するんだ。ただし、回帰の時は最小化すればよかったが、今回は最大化なので注意が必要だ。そこが違うので、ただ代入すればいいというわけじゃない。

やる夫
あ、確かにそうだお…もうすぐ終わりそうなのに、ここにきてまた壁がでてきたお。

やらない夫
そう難しく考えるな。最大化問題を最小化問題に置き換える簡単な方法がある。符号を反転させればいいだけだ。

やる夫
まじかお？

やらない夫
単純だろう。 $f(x)$ を最大化させる問題と、その符号を反転させた $-f(x)$ を最小化させる問題はまったく同じ問題だ。

やる夫
希望が見えてきたお。要するにこれまでは $\log L(\boldsymbol{\theta})$ を最大化することを考えてきたけど、これからは $-\log L(\boldsymbol{\theta})$ を最小化することを考えればいいってことかお？

やらない夫
その通りだ。符号が反転したんだから、微分結果の符号も反転する。 $L^{-}(\boldsymbol{\theta}) = -\log L(\boldsymbol{\theta})$ と置くと、こうなるな。

$\frac{\partial L^{-}(\boldsymbol{\theta})}{\partial \theta_j} = \sum_{i=1}^n \left(f_{\boldsymbol{\theta}}(\boldsymbol{x}) - y^{(i)} \right) x_j$

やる夫
てことは、パラメータ更新式は、こうかお？

$\theta_j := \theta_j - \eta \sum_{i=1}^n \left(f_{\boldsymbol{\theta}}(\boldsymbol{x}) - y^{(i)} \right) x_j$

やらない夫
よし、できたな。

線形分離不可能問題

やらない夫
では、いよいよ線形分離不可能な問題にも挑戦していこうか。

やる夫
待ってましたお。

やらない夫
これが線形分離不可能だということはもういいな？

やる夫
わかってるお。

やらない夫
線形分離不可能な問題は、すなわち直線では分離できないということだ。であれば、曲線で分離すればいいという発想に自然といきつく。

やる夫
お、もしかして多項式回帰の時にやったように、次数を増やしてみるってことかお？

やらない夫
勘がいいな。よし、これは 2 次元の話なので、素性としては $x_1$ と $x_2$ の 2 つがある。そこに 3 つ目の素性として $x_1^2$ を加える事を考えて見るんだ。

やる夫
こういうことかお？

$\boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \ \theta_1 \ \theta_2 \ \theta_3 \end{array} \right] \ \ \ \boldsymbol{x} = \left[ \begin{array}{c} 1 \ x_1 \ x_2 \ x_1^2 \end{array} \right]$

やらない夫
そうだな。つまり $\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x}$ はこうだ。大丈夫か？

$\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2$

やる夫
わかるお。

やらない夫
また適当に $\boldsymbol{\theta}$ を決めてみよう。そうだな、たとえば $\boldsymbol{\theta}$ がこうなった時、それぞれ $y=1$ と $y=0$ と分類される領域はどこになる？

$\boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \ \theta_1 \ \theta_2 \ \theta_3 \end{array} \right] = \left[ \begin{array}{c} 0 \ 0 \ 1 \ -1 \end{array} \right]$

やる夫
えーっと、要するに $\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x} \ge 0$ を考えればいいんだから…前と同じように変形してみるお。

$\begin{eqnarray} \boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x} = x_2 - x_1^2 & \ge & 0 \ x_2 & \ge & x_1^2 \end{eqnarray}$

やる夫
こんな感じかお？

やらない夫
その通りだ。以前は決定境界が直線だったが、今は曲線になっているのが見て取れるだろう。

やる夫
見た感じ、この決定境界だとまったく分類できてないように見えるけど、それはいつものようにやらない夫神が適当に $\boldsymbol{\theta}$ を決めたから、ってことでいいかお？

やらない夫
もう慣れてきたようだな。やる夫の言う通りだ。

やる夫
じゃ、これをさっき求めたパラメータ更新式を使って、 $\boldsymbol{\theta}$ を学習していけばいいってことかお。

やらない夫
これで線形分離不可能な問題も解けるようになったな。

やる夫
楽勝だお！

やらない夫
あとは、好きなように次数を増やせば複雑な形の決定境界にすることができる。たとえばさっきは素性として $x_1^2$ を増やしたが $x_2^2$ も増やすと、円状の決定境界ができる。

やる夫
ロジスティック回帰のパラメータ更新って、最初に回帰で考えた時と同じように全データで学習してるけど、ここにも確率的勾配降下法って使えるのかお？

やらない夫
もちろん使えるぞ。

やる夫
ロジスティック回帰って万能だお。

やらない夫
やる夫はいつも結論を出すのが早すぎだな。どんな問題に対しても万能なアルゴリズムなんて存在しないんだから適材適所で使っていかなければならない。

やる夫
今のやる夫はまだパーセプトロンとロジスティック回帰しか知らないんだから、ロジスティック回帰の方がやる夫にとっては有能な分類アルゴリズムだお。

やらない夫
それもそうだな。分類器はいろいろなアルゴリズムがあるから、勉強していくと楽しいぞ。

やる夫
自習なんて面倒くさいお…

やらない夫
本当に面倒くさがりなんだな、お前…

やる夫
天性だお。

やらない夫
自慢するところかよ。しかしこれまでだいぶ理論を説明してきたが、理論だけじゃなくて実際になにか作ってみることも大事だ。理解度が飛躍的に上がるぞ。

やる夫
じゃ、やっぱり前に言ってたアレ、作るお…

やらない夫
その熱意には負けるよ。

やる夫で学ぶ機械学習 - 過学習 - へ続く。

2016-06-06

やる夫で学ぶ機械学習シリーズ

　本シリーズ記事が書籍になりました。詳しくはこちら。

「やさしく学ぶ機械学習を理解するための数学のきほん」を執筆しました

これは、機械学習に関する基礎知識をまとめたシリーズ記事の目次となる記事です。まとめることで知識を体系化できて自分自身の為にもなるので、こういうアウトプットをすることは大事だと思っています。ただ、普通にブログ記事を書くのも面白くないので、ちょっといつもとは違う方法でやってみようというのが今回のシリーズ記事。

2 ちゃんねるのキャラクターが登場人物として出てきて、彼らが会話して話が進んでいく「やる夫で学ぶシリーズ」という講義調の形式のものがあります。個人的にはやる夫で学ぶシリーズや数学ガールのような会話形式で話が進んでいく読み物は読みやすいと思っています。さらに、先日みつけたやる夫で学ぶディジタル信号処理という資料がとてつもなくわかりやすく、これの真似をして書いてみようと思い至りました。記事中のやる夫とやらない夫のアイコンは http://matsucon.net/material/mona/ こちらのサイトの素材を使わせていただきました。

第 2 回まで半年ほど前に公開していましたが、その後ブログ執筆の熱が冷めて放置されていました。が、実は下書きだけなら乱雑ながら第 5 回までは書いていて、周りにいる機械学習入門中の知り合い数名から下書きあるなら公開して欲しいと言われたので、お蔵入りさせるのも勿体ないし一気に清書して、この目次記事をつけて公開することにしました。今後、このシリーズ記事が増えるかどうかはわかりません。

まえがき

このシリーズでは実践的な内容というよりかは、基礎的で理論的な部分をまとめていきます。機械学習をやり始めるにあたってまず最初にやったほうが良いのは、こういった座学のような記事を頑張って読むよりかは、やってみた系の記事を読みながら実際に手を動かしてコーディングしてみることです。いきなり機械学習の本や数式を眺めて理論から理解し始めるのは、数学に自信がある人や素養がある人以外は難しく、挫折してしまう原因となります。

今は良い時代になっていて、フレームワークを基盤として少しのコードを書いて、公開されている無料の学習用データを使えば、それらしいものが出来てしまいます。そういうもので感覚を掴んでから、理論を理解するのでも遅くはないと思っています。

とはいえ、プログラマであれば中身を知らないものをアレコレ触るのは怖さがあるというもの。理論の方に手をだしてみたくなったりもします。座学系の記事は、このブログ以外にもたくさん転がっているのでイロイロ読み比べて知識を自分のものにしていくのが大事です。一晩でなんとかなるものでもないですし、じっくりやっていきましょう。

対象

機械学習って最近よく聞くけど中身を良くしらない人
中身しらないけど機械学習って楽しそうだしなんか勉強してみたい人
数学が好きな人
ドヤ顔で機械学習のことを話したい人

※上級者向けではありません。どちらかというとむしろ初学者向けです。

やる夫で学ぶ機械学習 - ロジスティック回帰 -

やる夫で学ぶ機械学習シリーズの第 5 回です。分類問題を解くためのロジスティック回帰を見ていきます。

第 4 回はこちら。やる夫で学ぶ機械学習 - パーセプトロン -

目次はこちら。やる夫で学ぶ機械学習シリーズ

ロジスティック回帰

やる夫
分類問題を解くための素晴らしいアルゴリズムがあると聞きましたお。

やらない夫
今日は展開が早いな。

やる夫
回りくどいのは終わりだお。

やらない夫
では、今日はロジスティック回帰の話をしていこう。ロジスティック回帰は、パーセプトロンのように基本的には二値分類の分類器を構築するためのものだ。

やる夫
パーセプトロンよりは使い物になるのかお？

やらない夫
もちろんさ。ロジスティック回帰はいろんなところで使われているし、線形分離不可能な問題も解ける。

やる夫
それはナイスだお。

やらない夫
いつものように最初は簡単な具体例を示して概要を見ていこうか。

やる夫
よろしくお願いしますお。

やらない夫
問題設定はパーセプトロンの時と同じものを使おう。つまり、色を暖色か寒色に分類することを考えるんだ。

やる夫
それ、線形分離可能な問題だお？線形分離不可能な問題やらないのかお？

やらない夫
物事には順序ってものがあるだろう。先に基礎からやるんだよ。ロジスティック回帰も、もちろん線形分離可能な問題は解ける。まずそこから入って、その応用で最後に線形分離不可能な問題を見ていこう。

やる夫
基礎力つけるの面倒くさいけど、わかったお…

やらない夫
ロジスティック回帰は分類を確率として考えるんだ。

やる夫
確率？暖色である確率が 80%、寒色である確率が 20%、みたいな話ってことかお？

やらない夫
そうだ、いつもとぼけた顔してる割には冴えてるじゃないか。

やる夫
顔は生まれつきだお。文句いうなお。

やらない夫
暖色、寒色のままでは扱いにくいのはパーセプトロンと同じだから、ここでは暖色を $1$ 、寒色を $0$ と置くとしよう。

やる夫
あれ、寒色は $-1$ じゃないのかお？

やらない夫
クラス毎の値が異なっていれば別になんでもいいんだが、パーセプトロンの時に暖色が $1$ で寒色が $-1$ にしたのは、そうした方が重みの更新式が簡潔に書けるからだ。

やる夫
なるほど。ロジスティック回帰の場合は暖色を $1$ で寒色を $0$ にした方が、重みの更新式が簡潔に書き表せるってことかお？

やらない夫
そういうことだな。話を進めよう。回帰の時に、未知のデータ $\boldsymbol{x}$ に対応する値を求めるためにこういう関数を定義したのを覚えているか？

$f_{\boldsymbol{\theta}}(\boldsymbol{x}) = \boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x}$

やる夫
覚えてるお。学習用データに最も良くフィットするパラメータ $\boldsymbol{\theta}$ を求めた時だお。あの時は最急降下法か確率的勾配降下法を使ってパラメータ $\boldsymbol{\theta}$ の更新式を導出したんだったお。

やらない夫
ロジスティック回帰でも考え方は同じだ。未知のデータがどのクラスに分類されるかを求めたい時に、それを分類してくれるための関数が必要になるな。

やる夫
パーセプトロンでやった時の識別関数 $f_{\boldsymbol{w}}$ みたいなもんかお？

やらない夫
そうだな。今回も回帰の時と同じように $\boldsymbol{\theta}$ を使うことにして、ロジスティック回帰の関数をこのように定義しよう。

$f_{\boldsymbol{\theta}}(\boldsymbol{x}) = \frac{1}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}$

やる夫
急に難易度が上がるのは、このシリーズのセオリーかお。

やらない夫
ぱっと見て難しそうだと感じるのはわかるが、落ち着いて考えるんだ。第一印象で無理かどうかを決めるのは良くないぞ。

やる夫
$\exp(x)$ ってのは $\mathrm{e}^x$ ってことかお？

やらない夫
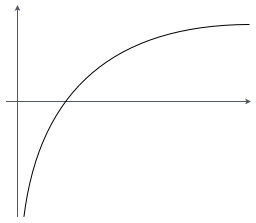
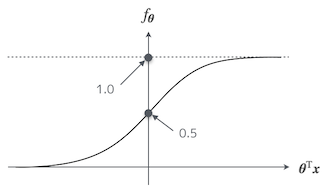
そうだ。この関数は一般的にシグモイド関数と呼ばれるんだが、 $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}$ を横軸、 $f_{\boldsymbol{\theta}}$ を縦軸だとすると、グラフの形はこんな風になっている。

やる夫
お、ものすごくなめらかな形をしているお。

やらない夫
特徴としては、 $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} = 0$ の時に $f_{\boldsymbol{\theta}} = 0.5$ になっている。それから、グラフを見ればすぐわかると思うが $0 \le f_{\boldsymbol{\theta}} \le 1$ だ。

やる夫
グラフの形なんか示してどうするんだお。

やらない夫
目に見えるように表現すると見えないモノが見えてくる。今は、分類を確率で考えようとしているんだ。覚えているか？

やる夫
覚えてるお。あ…そうか、シグモイド関数は $0 \le f_{\boldsymbol{\theta}} \le 1$ だから確率として扱える、ってことかお。

やらない夫
その通りだ。ここからは、未知のデータ $\boldsymbol{x}$ が暖色、つまり $y=1$ である確率を $f_{\boldsymbol{\theta}}$ とするんだ。

$P(y=1|\boldsymbol{x}) = f_{\boldsymbol{\theta}}(\boldsymbol{x})$

やらない夫
具体例を見てみようか。そうだな、 $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ を計算すると $0.7$ になったとしよう。これはどういう状態だ？

やる夫
あ、えーっと… $f_{\boldsymbol{\theta}}(\boldsymbol{x}) = 0.7$ ってことは、暖色である確率が 70% ってことかお？逆に寒色である確率は 30%。普通に考えて $\boldsymbol{x}$ は暖色ってことになるお。

やらない夫
では今度は、 $f_{\boldsymbol{\theta}}(\boldsymbol{x}) = 0.2$ の時はどうだろう。

やる夫
暖色が 20% で、寒色が 80% だから $\boldsymbol{x}$ は寒色だお。

やらない夫
やる夫は今おそらく、 $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ の閾値を $0.5$ としてクラスを振り分けているはずだ。

$\begin{eqnarray} y = \begin{cases} 1 & (f_{\boldsymbol{\theta}}(\boldsymbol{x}) \ge 0.5) \\[5pt] 0 & (f_{\boldsymbol{\theta}}(\boldsymbol{x}) < 0.5) \end{cases} \end{eqnarray}$

やる夫
あぁ、別に意識はしてなかったけど、確かにそうだお。 $f_{\boldsymbol{\theta}}(\boldsymbol{x}) \ge 0.5$ なら暖色だと思うし、逆は寒色だお。

やらない夫
$f_{\boldsymbol{\theta}}(\boldsymbol{x}) \ge 0.5$ というのは、もっと詳しく見るとどういう状態だ？シグモイド関数のグラフを思い出して考えてみるんだ。

やる夫
んー…？シグモイド関数は $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} = 0$ の時に $f_{\boldsymbol{\theta}}(\boldsymbol{x}) = 0.5$ だったお…あっ、要するに $f_{\boldsymbol{\theta}}(\boldsymbol{x}) \ge 0.5$ ってことは $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} \ge 0$ ってことかお？

やらない夫
正解だ。さっきの場合分けの条件式の部分を書き直すとこうだな。

$\begin{eqnarray} y = \begin{cases} 1 & (\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} \ge 0) \\[5pt] 0 & (\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} < 0) \end{cases} \end{eqnarray}$

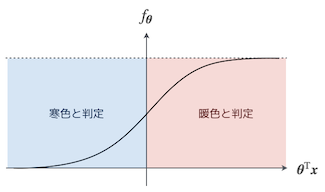
やらない夫
シグモイド関数のグラフをみると、こんな風に分類される感じだな。

やる夫
なるほど、わかりやすいお。でも、条件式の部分って $f_{\boldsymbol{\theta}}(\boldsymbol{x}) \ge 0.5$ でも $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} \ge 0$ でも同じ意味ならなんでわざわざ書き直すんだお？

やらない夫
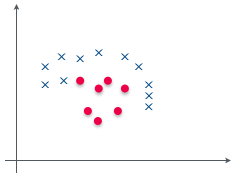
では、今度はパーセプトロンの時に見たような、横軸が赤( $x_1$ )、縦軸が青( $x_2$ ) のグラフを考えてみようか。

やる夫
あぁ、色をプロットしていたアレかお。

やらない夫
今回の問題、素性としては赤 ( $x_1$ ) と青 ( $x_2$ ) の 2 次元だが、回帰の時と同じように $\theta_0$ と $x_0$ も含めて、全体としては 3 次元ベクトルで考えるぞ。いいか？

やる夫
大丈夫だお。 $x_0 = 1$ は固定だったお。

やらない夫
具体的に考えるために、適当にパラメータ $\boldsymbol{\theta}$ を決めよう。そうだな、こういう $\boldsymbol{\theta}$ があった時、暖色である場合の条件式 $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} \ge 0$ をグラフに表すとどうなる？

$\boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \\ \theta_1 \\ \theta_2 \end{array} \right] = \left[ \begin{array}{c} -100 \\ 2 \\ 1 \end{array} \right]$

やる夫
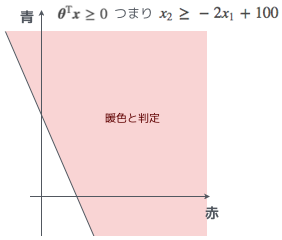
ん、条件式をグラフに…とりあえず $\boldsymbol{\theta}$ を代入して、わかりやすいように変形してみるお…

$\begin{eqnarray} \boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} = -100 + 2 x_1 + x_2 & \ge & 0 \ x_2 & \ge & - 2 x_1 + 100 \end{eqnarray}$

やる夫
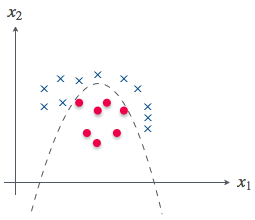
これをグラフに…こうかお？

やらない夫
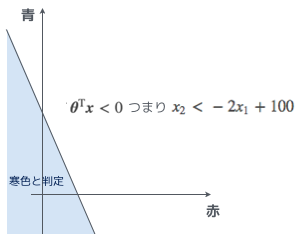
ここまでくれば $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} < 0$ の場合がどうなるかも想像できるな？

やる夫
今度はさっきの反対側ってことかお。

やらない夫
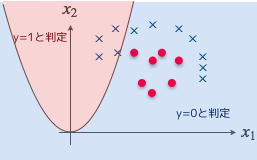
つまり $\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} = 0$ という直線を境界線として、一方が暖色( $y=1$ )、もう一方が寒色( $y=0$ )、とクラス分けできるというわけだ。

やる夫
これは直感的でわかりやすいお！パーセプトロンの時にも $\boldsymbol{w} \cdot \boldsymbol{x} = 0$ というクラスを分類するための線が出てきたけど、それと同じものってことかお。

やらない夫
そうだな。このようなクラスを分割する線を決定境界、英語では Decision Boundary と呼ぶ。

やる夫
この決定境界、暖色と寒色を分類する線としては全く正しくなさそうだけど、それはやらない夫が適当にパラメータの $\boldsymbol{\theta}$ を決めたから、ってことかお？

やらない夫
そういうことだ。ということは、これから何をやっていくのかは、想像つくだろう？

やる夫
正しいパラメータ $\boldsymbol{\theta}$ を求めるために、目的関数を定義して、微分して、パラメータの更新式を求める、であってるかお？

やらない夫
よくわかってるじゃないか。

尤度関数

やる夫
あとは回帰と同じなら楽勝だお。今日はもう帰ってオンラインゲームでもやるお。

やらない夫
そうだったら良かったんだが、世の中そんなに甘くないぞ。

やる夫
はっ…そういえば今日は週 1 のメンテナンス日だったお…

やらない夫
お前、そういうことじゃないだろ、常識的に考えて…。ロジスティック回帰は、二乗誤差の目的関数だとうまくいかないから別の目的関数を定義するんだ。最初にやった回帰と同じ手法ではやらない。

やる夫
そうなのかお…帰ってもやることないから、やらない夫の講義に付き合ってやるお。

やらない夫
その上から目線、癪に障るが…ロジスティック回帰の目的関数を考えよう。パーセプトロンの時に準備した学習用データについて、さっき俺が適当に決めたパラメータ $\boldsymbol{\theta}$ を使って、実際に $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ を計算してみよう。ここで示す $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ の計算結果は全く厳密ではないが、イメージをつかむにはそれで十分だろう。

色	クラス	$y$	$f_{\boldsymbol{\theta}}(\boldsymbol{x})$
#d80055	暖色	1	0.00005
#c80027	暖色	1	0.00004
#9c0019	暖色	1	0.00002
#2c00c8	寒色	0	0.99991
#120078	寒色	0	0.99971
#40009f	寒色	0	0.99953

やらない夫
$f_{\boldsymbol{\theta}}(\boldsymbol{x})$ は $\boldsymbol{x}$ が暖色である確率だと定義した。これは覚えているな。

やる夫
大丈夫だお。

やらない夫
では、それを踏まえた上で、 $y$ と $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ はどういう関係にあるのが理想的だと思う？

やる夫
えっ、えーっと… $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ は $\boldsymbol{x}$ が暖色である確率なんだから…正しく分類されるためには、 $y=1$ の時に $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ が $1$ に近くて、 $y=0$ の時に $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ が $0$ に近い方がいい、ってことかお？

やらない夫
そうだな。理想の状態はやる夫の言った通りで正解だが、以下のようにも言い換えることができる。

$y=1$ の時は $P(y=1|\boldsymbol{x})$ が最大になって欲しい
$y=0$ の時は $P(y=0|\boldsymbol{x})$ が最大になって欲しい

やる夫
$P(y=1|\boldsymbol{x})$ は $\boldsymbol{x}$ が暖色である確率、逆に $P(y=0|\boldsymbol{x})$ が $\boldsymbol{x}$ が寒色である確率、という理解であってるかお？

やらない夫
それでいい。これを全ての学習用データについて考えるんだ。すると目的関数は以下のような同時確率として考えることができる。これを最大化する $\boldsymbol{\theta}$ を見つけることが目的だ。

$L(\boldsymbol{\theta}) = \prod_{i=1}^n P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}}$

やる夫
さて、帰るお。

やらない夫
期待通りの反応をありがとう。

やる夫
どうやったらこんな意味不明な式が思いつくんだお…。

やらない夫
確かに、式を簡潔にするために多少トリックを使ってはいるが、やる夫でも理解できるはずだ。1 つずつ考えよう。

やる夫
やらない夫の丁寧な説明をお待ちしておりますお。

やらない夫
$y^{(i)}$ が $1$ と $0$ の場合をそれぞれ考えてみよう。 $y^{(i)}=1$ のデータの場合は後ろ側の $P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}}$ が $1$ になる。逆に $y^{(i)}=0$ のデータの場合は前の $P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}}$ が $1$ になる。

やる夫
ん、なんでだお？

やらない夫
両方とも 0 乗になるだろう。 $P(y^{(i)}=1|\boldsymbol{x})$ や $P(y^{(i)}=0|\boldsymbol{x})$ がどんな数だったとしても、べき乗のところが 0 になるからだ。 $P(y^{(i)}=1|\boldsymbol{x})^0$ も $P(y^{(i)}=0|\boldsymbol{x})^0$ も両方とも 0 乗なんだから、1 になるのは明確だ。

やる夫
あ、なるほど。確かに、言われてみればそうだお。

やらない夫
まとめるとこうだ。

$y^{(i)}=1$ の時は $P(y^{(i)}=1|\boldsymbol{x})$ の項が残る
$y^{(i)}=0$ の時は $P(y^{(i)}=0|\boldsymbol{x})$ の項が残る

やらない夫
つまり全ての学習用データにおいて、正解ラベルと同じラベルに分類される確率が最大になるような同時確率を考えているということだ。

やる夫
うーん、わかったようなわかってないような…前の回帰の時は目的関数の最小化だったけど、今回は最大化するのかお。

やらない夫
そうだな。二乗誤差はその名の通り “誤差” なので小さいほうが理想的だ。だが、今回は同時確率だ。その同時確率が最も高くなるようなパラメータ $\boldsymbol{\theta}$ こそ、学習用データにフィットしていると言える。そういった、尤もらしいパラメータを求めたいんだ。

やる夫
国語のお勉強も足りてないお…それなんて読むんだお。

やらない夫
“尤もらしい” は “もっともらしい” と読む。さっき定義した関数も、尤度関数とも呼ばれる。これは “ゆうどかんすう” だな。目的関数に使った文字 $L$ も、尤度を英語で表した時の $Likelihood$ の頭文字から取った。

やる夫
やっぱり、ここにきて難易度あがってるお。面倒くさいけど、あとで復習するお…

やらない夫
そうだな。どうせ家に帰ってやることがないんだろう。

やる夫
バカにするなお…

やる夫で学ぶ機械学習 - 対数尤度関数 - へ続く。