やる夫で学ぶ機械学習シリーズの第 4 回です。分類問題を解くための基礎、パーセプトロンを図形的な側面から覗いてみます。
第 3 回はこちら。やる夫で学ぶ機械学習 - 多項式回帰と重回帰 -
目次はこちら。やる夫で学ぶ機械学習シリーズ
問題設定
![]() やらない夫
やらない夫
今日は分類問題について詳しく見ていく。
![]() やる夫
やる夫
分類問題かお。やる夫は、女の子が巨乳か貧乳かを分類して、想像を膨らませたいお。
![]() やらない夫
やらない夫
そんなものは深夜に一人でニヤニヤしながらやるか、いつも引きこもってないで外に出て本物の女の子を見ることだな。
![]() やる夫
やる夫
冗談きついお、やらない夫。
![]() やらない夫
やらない夫
分類の場合も、回帰の時と同じように具体例を示して、それを元に話を進めていったほうがわかりやすいな。
![]() やる夫
やる夫
それが良いお。具体例は、やる夫の将来の嫁さんくらい大事だお。
![]() やらない夫
やらない夫
また意味のわからないたとえをありがとう。今回は分類の話なので、そうだな、色を分類することを考えてみよう。
![]() やる夫
やる夫
おっぱいじゃなくて、色を分類、するのかお?
![]() やらない夫
やらない夫
おっぱいは忘れろ。たとえば、適当に与えられた色が、暖色系なのか寒色系なのかに分類する、という問題はどうだ?
![]() やる夫
やる夫
二値分類の問題かお。分類は確か教師あり学習だったから、つまりラベル付きの学習用データが要るってことかお?
![]() やらない夫
やらない夫
そうだな、具体的には、色の情報と、その色が暖色なのか寒色なのか、というラベルを学習用データとして用意してやる必要がある。
![]() やる夫
やる夫
なるほど。
![]() やらない夫
やらない夫
ところで、色と言えば RGB の三色を考えることができるが、最初は簡単な問題の方がいいから、緑のことは考えずに、赤と青だけに注目していこう。緑の要素は 0 に固定しようか。その方が図にもプロットできてわかりやすいしな。
![]() やる夫
やる夫
簡単になるなら歓迎だお。
![]() やらない夫
やらない夫
たとえば、この色は暖色系、寒色系、どっちに見える?
![]() やる夫
やる夫
んー、暖色系だお。
![]() やらない夫
やらない夫
では、これはどうだ?
![]() やる夫
やる夫
寒色系だお。
![]() やらない夫
やらない夫
ということは、今 2 つの学習用データができた。緑の要素を 0 に固定しているから、#RRGGBB の GG の部分が 00 になっていることに注目だ。
| 色 | クラス |
|---|---|
| #d80055 | 暖色 |
| #2c00c8 | 寒色 |
![]() やる夫
やる夫
うん、分類問題の場合の学習用データのイメージつかめたお。
![]() やらない夫
やらない夫
横軸を赤、縦軸を青、とすると、今の学習用データはこんな風にプロットできる。大丈夫か?
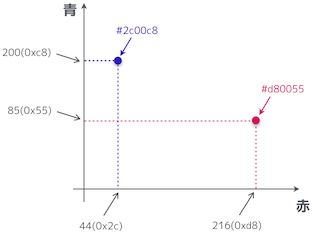
![]() やる夫
やる夫
楽勝だお。
![]() やらない夫
やらない夫
さすがに、学習用データが 2 つしかないと足りないので、もう少し増やしておこう。
| 色 | クラス |
|---|---|
| #d80055 | 暖色 |
| #c80027 | 暖色 |
| #9c0019 | 暖色 |
| #2c00c8 | 寒色 |
| #120078 | 寒色 |
| #40009f | 寒色 |
![]() やる夫
やる夫
プロットしてみたお。
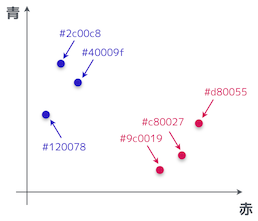
![]() やらない夫
やらない夫
よし、OK だ。この図を見て、このデータ点を分類するために 1 本だけ線を引くとしたら、やる夫はどんな風に線を引く?
![]() やる夫
やる夫
ん、そんなの、誰でもこんな風に線を引くと思うお。
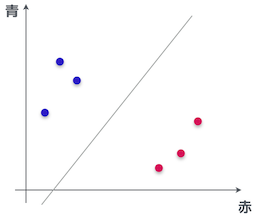
![]() やらない夫
やらない夫
よし。今回の目的はその線を見つけること、それが二値分類だ。
内積
![]() やる夫
やる夫
線をみつけるって、つまり回帰の時と同じように一次関数の傾きと切片を求めるのかお?
![]() やらない夫
やらない夫
いや、今回はベクトルを見つけるのが目的だ。
![]() やる夫
やる夫
ベクトルを見つける…。やらない夫、意味がわからんお…。
![]() やらない夫
やらない夫
さっきの線は、重みベクトルを法線とする直線なんだ。重みベクトルを $\boldsymbol{w}$ とすると、直線の方程式はこのように表せる。
$$ \boldsymbol{w}\cdot\boldsymbol{x} = 0 $$
![]() やる夫
やる夫
うーん、重みベクトルって一体なんなんだお…、その方程式の意味もよくわからんお。
![]() やらない夫
やらない夫
重みベクトルは俺たちが知りたい未知のパラメータだ。回帰の時に $\boldsymbol{\theta}$ という未知のパラメータを求めるために色々と頑張ったが、それと同じものだな。$w$ という文字は weight(重み) の頭文字だ。
![]() やる夫
やる夫
$\boldsymbol{w}\cdot\boldsymbol{x}$ って、ベクトルの内積のことかお?
![]() やらない夫
やらない夫
そう、内積のことだ。実ベクトル空間の内積は、各要素の積を足し上げたものなので、こんな風にも書ける。$n$ は次元数だ。
$$ \boldsymbol{w}\cdot\boldsymbol{x} = \sum_{i=1}^n w_i x_i = 0 $$
![]() やる夫
やる夫
ふむ。今回は赤と青の二次元を考えているので、$n = 2$ ってことでいいのかお。
![]() やらない夫
やらない夫
そういうことだ。
![]() やる夫
やる夫
うーん、内積は覚えてるけど、でも、さっきの方程式…、なんなんだお。
![]() やらない夫
やらない夫
わからない時はいつでも、具体的な値を代入して計算してみよう。イメージがわくかもしれないぞ。やる夫が言ったように、今回の問題は $\mathbb{R}^2$ の実ベクトル空間上で考えているので、そうだな、重みベクトルを $\boldsymbol{w} = (1, 1)$ とした時、$\boldsymbol{x}$ はどうなる?
![]() やる夫
やる夫
とりあえず、代入してみるお。
\begin{eqnarray}
\boldsymbol{w}\cdot\boldsymbol{x} & = & w_1 x_1 + w_2 x_2 \
& = & 1\cdot x_1 + 1\cdot x_2 \
& = & x_1 + x_2 = 0
\end{eqnarray}
![]() やる夫
やる夫
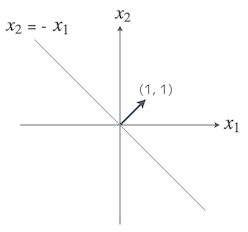
ん、これって要するに $x_2 = -x_1$ だから、$\boldsymbol{x} = (1, -1)$ とか $\boldsymbol{x} = (2, -2)$ とか、解は無限にありそうだけど…、あー、つまり、傾き -1 のグラフってことかお?
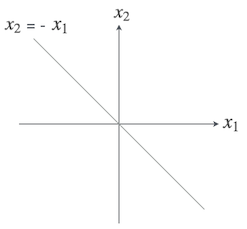
![]() やらない夫
やらない夫
よく閃いたな。その図に、重みベクトル $\boldsymbol{w} = (1, 1)$ を書き加えてみると、もっとわかりやすいかもしれないな。
![]() やる夫
やる夫
えっと、$(1, 1)$ だから…
![]() やる夫
やる夫
あっ、重みベクトル $\boldsymbol{w}$ が、さっきやる夫が書いた直線と、直角になってるお。
![]() やらない夫
やらない夫
つまり重みベクトル $\boldsymbol{w}$ が、やる夫が書いた直線に対する法線になっているというわけだ。最初に俺が言ったように、$\boldsymbol{w}\cdot\boldsymbol{x} = 0$ という式は、重みベクトル $\boldsymbol{w}$ を法線とする直線の方程式になっている。
![]() やる夫
やる夫
そういうことかお。そういえば、内積の計算って $\cos$ が含まれてなかったかお?ベクトル同士の成す角 $\theta$ を使って..
$$ \boldsymbol{w}\cdot\boldsymbol{x} = |\boldsymbol{w}|\cdot|\boldsymbol{x}|\cdot\cos\theta $$
![]() やらない夫
やらない夫
それでも問題ない。さっき、やる夫はベクトル方程式から代数的に解いたが、幾何的にはベクトル同士が直角になっている時に内積が 0 になる。$\theta = 90^{\circ}, 270^{\circ}$ の時には $\cos\theta = 0$ になるからな。
![]() やる夫
やる夫
あーなるほど。そういう直角になってるベクトルがたくさんあって、それ全体が直線になってるのかお。
![]() やらない夫
やらない夫
いろんな側面から覗いてみると、より理解も深まる。
![]() やる夫
やる夫
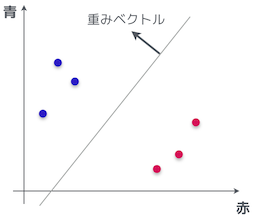
じゃ、話は戻るけど、さっきの色分類の問題に関するグラフで言うと、こんな風にやる夫が引いた直線に対する法線を見つける、ってことかお。
![]() やらない夫
やらない夫
そういうことだ。まあ正確にはもちろん最初に直線があるわけではなく、最初に法線、つまり重みベクトルを見つけると、そのベクトルに対して直角な直線がわかり、その直線によってデータが分類される、というわけだな。
![]() やる夫
やる夫
把握したお。
パーセプトロン
![]() やる夫
やる夫
で、具体的にはどうやって、その重みベクトルとやらを求めるのかお?
![]() やらない夫
やらない夫
回帰でやった時のように、重みベクトルをパラメータとして、パラメータを更新していくんだ。これから見ていくのは、パーセプトロンと呼ばれるモデルだ。
![]() やる夫
やる夫
なんか突然かっこいい単語が出てきたお。
![]() やらない夫
やらない夫
パーセプトロンは脳の機能を参考にモデル化したものだと言われることが多いな。ローゼンブラットという人物が考案したモデルなんだ。
![]() やる夫
やる夫
今度は RPG の主人公キャラの名前かお。
![]() やらない夫
やらない夫
パーセプトロンは複数の入力を受け取り、その入力に対する重みとの線形結合が一定の閾値を超えていた場合に活性化し、そうでない場合は非活性となるような単純な関数だ。
![]() やる夫
やる夫
線形結合とか活性化とか非活性とか、一体やらない夫は何を言ってるんだお。中二病なのかお。
![]() やらない夫
やらない夫
いや、そういうわけではないが…。そうだな、つまらない形式的な話はよしておこう。形式的な話より直感的な話をしていこうか。やる夫もそっちの方が好きだろう。
![]() やる夫
やる夫
それでいいんだお。ところで、パラメータの更新っていうと、また微分とか出てくるのかお。
![]() やらない夫
やらない夫
あの時は目的関数があって、それを最小化したいがために微分したんだった。だが、今回は目的関数は不要なので、微分もしない。
![]() やる夫
やる夫
なるほど。分類も回帰と同じ流れかと思ったけど、そうでもないのかお。
![]() やらない夫
やらない夫
分類問題でも、もちろん目的関数を使うこともあって、その場合には目的関数を最小化する手順は同じようにある。ただ、パーセプトロンのように目的関数が必要ないような場合もある。
![]() やる夫
やる夫
ふーん。じゃ、今回のパラメータの更新式は、どんなものになるんだお?
![]() やらない夫
やらない夫
その前に、パラメータ更新に必要になるものを、いくつか準備をしておこう。
![]() やる夫
やる夫
うっ、前準備って、面倒くさくてあんまり好きじゃないお…
![]() やらない夫
やらない夫
このまま先に進んでも、どうせやる夫はわからないだろうからな。まあ、そんなにたくさん準備がいるわけじゃないから安心しろ。
![]() やる夫
やる夫
やらない夫、いま、しれっとやる夫のこと馬鹿にしたお…
![]() やらない夫
やらない夫
まず、最初に用意した学習用データの、暖色と寒色。このままだと扱いにくいから、暖色を 1、寒色を -1 として、$y$ で表すことにする。そして、横軸を赤、縦軸を青、としていたが、それぞれ $x_1$ と $x_2$ としよう。
| 色 | クラス | $x_1$ | $x_2$ | $y$ |
|---|---|---|---|---|
| #d80055 | 暖色 | 216 | 85 | 1 |
| #c80027 | 暖色 | 200 | 39 | 1 |
| #9c0019 | 暖色 | 156 | 25 | 1 |
| #2c00c8 | 寒色 | 44 | 200 | -1 |
| #120078 | 寒色 | 18 | 120 | -1 |
| #40009f | 寒色 | 64 | 159 | -1 |
![]() やらない夫
やらない夫
そして、ベクトル $\boldsymbol{x}$ を与えると、暖色か寒色を判定する関数、つまり 1 または -1 を返す関数 $f_{\boldsymbol{w}}$ をこのように定義する。このような関数を「識別関数」と呼ぶ。
\begin{eqnarray} f_{\boldsymbol{w}}(\boldsymbol{x}) = \begin{cases} 1 & (\boldsymbol{w}\cdot\boldsymbol{x} \geq 0) \\[5pt] -1 & (\boldsymbol{w}\cdot\boldsymbol{x} \lt 0) \end{cases} \end{eqnarray}
![]() やる夫
やる夫
ん、要するに内積の符号によって返す値が違うってことかお。こんなんで、暖色か寒色が判定できるのかお?
![]() やらない夫
やらない夫
内積の図形的なイメージを思い出すんだ。例えば、重みベクトル $\boldsymbol{w}$ に対して、内積が負になるベクトルってどんなベクトルだ?$\cos$ が含まれた方の式で考えてみるんだ。
![]() やる夫
やる夫
ん、$\cos$ を使った内積は $|\boldsymbol{w}|\cdot|\boldsymbol{x}|\cdot\cos\theta$ だから…、ベクトルの大きさは必ず正になるから、符号は $\cos\theta$ の値で決まることになるお…、これが負になるってことは、$90^{\circ} \lt \theta \lt 270^{\circ}$ の場合、ってことかお?
![]() やらない夫
やらない夫
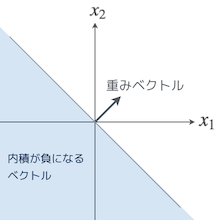
正解だ。そういうベクトル $\boldsymbol{x}$ は、図形的にはどんな位置にあると思う?
![]() やる夫
やる夫
重みベクトル $\boldsymbol{w}$ との成す角が $90^{\circ} \lt \theta \lt 270^{\circ}$ の範囲内にあるベクトルってことだから…、あー、なるほど、直線を挟んで重みベクトルとは反対側の部分、ってことかお。
![]() やらない夫
やらない夫
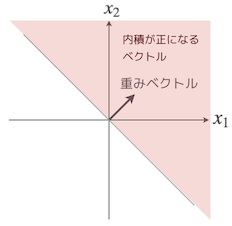
その通り。と、いうことは、内積が正のベクトルは、重みベクトルと同じ側の部分ってことだな。
![]() やる夫
やる夫
なるほど!内積が正か負かで、直線を挟んで分割できてるお。
![]() やらない夫
やらない夫
内積は、ベクトル同士がどれだけ似ているかという指標にも使われる。符号が正だとある程度似ていて、0 で直角になり、そして負になると、だんだん元のベクトルから離れていく。
![]() やる夫
やる夫
内積にはそういう意味もあったのかお。
![]() やらない夫
やらない夫
さて、準備はこれで終わりだ。話を戻すと、パラメータの更新式はこのように定義する。$i$ は学習用データのインデックスだ。このパラメータ更新を全ての学習用データについて行っていく。
\begin{eqnarray} \boldsymbol{w} := \begin{cases} \boldsymbol{w} + y^{(i)}\boldsymbol{x}^{(i)} & (f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) \neq y^{(i)}) \\[5pt] \boldsymbol{w} & (f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) = y^{(i)}) \end{cases} \end{eqnarray}
![]() やる夫
やる夫
んー、なんかまた、ごちゃごちゃした式だお…
![]() やらない夫
やらない夫
意味がわからない数式を見た時は、いったん落ち着くんだ。難しそうな式がごちゃごちゃしているのは確かだが、その式の文字を 1 つずつ読み解いていき、ボトムアップで全体像を把握していけばいい。
![]() やる夫
やる夫
んっと、じゃ、まずは $f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) \neq y^{(i)}$ の方から見ていくお…
![]() やらない夫
やらない夫
それがいい。その条件は、どういうことを表していると思う?
![]() やる夫
やる夫
$i$ 番目の学習用データを識別関数に通して分類した結果と、同じく $i$ 番目の学習用データのラベル $y$ が異なっている、ってことだお。あ、ということは、識別関数による分類に失敗した、ってことなのかお?
![]() やらない夫
やらない夫
やるじゃないか、やる夫の言う通りだ。
![]() やる夫
やる夫
もう一つの $f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) = y^{(i)}$ の方は、逆に分類に成功した、って意味だお。
![]() やらない夫
やらない夫
そういうことだ。つまり、先のパラメータ更新式は、識別関数による分類が失敗した時だけ新しいパラメータに更新されるという意味だ。分類に成功した場合は、パラメータの重みベクトルは正しいはずだと捉えて更新をしない。そこ、大丈夫か?
![]() やる夫
やる夫
わかるお。分類が成功した時、つまり $f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) = y^{(i)}$ の時は $\boldsymbol{w}$ がそのまま代入されて、元と何も変わってないから、そういうことだお。
![]() やらない夫
やらない夫
では今度は、識別関数による分類が失敗した時の更新式を見てみようか。
![]() やる夫
やる夫
$\boldsymbol{w} + y^{(i)}\boldsymbol{x}^{(i)}$ の方かお。うーん…、さっきから考えてるけど、未だにまったく意味がわからんお…。
![]() やらない夫
やらない夫
式だけ眺めてても難しいかもしれないな。こちらも図形的に考えてみるといい。
![]() やる夫
やる夫
グラフに書いてみるってことかお。ん、でも、そんな式どうやって図に書けばいいのかお?
![]() やらない夫
やらない夫
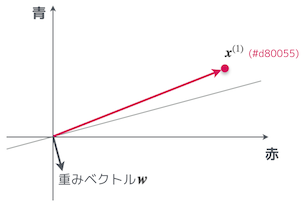
具体例を考えるんだよ。まずは、以下の図にあるような適当な重みベクトルがあったとして、その状態でラベルが $y = 1$、つまり暖色系の学習用データを与えた場合にどうなるかを考えてみよう。
![]() やる夫
やる夫
上の図の場合、重みベクトル $\boldsymbol{w}$ と学習用データ $\boldsymbol{x}^{(1)}$ との成す角は $90^{\circ}$ 以上だから内積が負になって、識別関数 $f_{\boldsymbol{w}}$ は -1 を返すはずだお。そして、与えられた学習用データのラベルは $y = 1$ だから、識別関数による分類に失敗しているお。
![]() やらない夫
やらない夫
パラメータ更新式の $f_{\boldsymbol{w}}(\boldsymbol{x}^{(1)}) \neq y^{(1)}$ という状況だな。つまり、パラメータが更新されるというわけだ。
![]() やる夫
やる夫
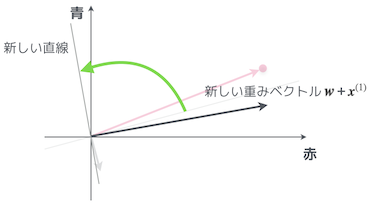
なるほど。いま、$y^{(1)} = 1$ だから、更新式は $\boldsymbol{w} + \boldsymbol{x}^{(1)}$ になるわけだお。んー、普通のベクトルの足し算だから、さっきの図に書き足してみるお…
![]() やる夫
やる夫
重みベクトル $\boldsymbol{w}$ が更新されて、最初に引いてた直線が回転したお!
![]() やらない夫
やらない夫
新しい重みベクトルの元で識別関数に通すと、今度はちゃんと分類に成功することもわかるだろう。
![]() やる夫
やる夫
さっきは、$\boldsymbol{x}^{(1)}$ が直線を挟んで重みベクトルと反対側にあったけど、新しい重みベクトルで見た場合、$\boldsymbol{x}^{(1)}$ は重みベクトルと同じ側にあるから確かに良さそうだお。
![]() やらない夫
やらない夫
学習用データのラベルが $y = -1$ の場合は、今度はパラメータ更新がベクトルの引き算になるわけだな。
![]() やる夫
やる夫
足し算と引き算の違いはあるけど、同じように新しい重みベクトルに更新されて、その分だけ直線が回転するってことかお。
![]() やらない夫
やらない夫
この繰り返しによってパラメータを更新していくのがパーセプトロンの学習だ。
![]() やる夫
やる夫
とてもよくわかりましたお。顔画像を準備して、巨乳なら 1、そうじゃないなら -1 ってラベルをつけていけば、未知の女の子をパーセプトロンで分類できそうだお。
![]() やらない夫
やらない夫
お前、まだそれ諦めてなかったのかよ…そんなものはおそらくパーセプトロンでは分類できないだろうな。
線形分離可能
![]() やる夫
やる夫
またやる夫のことバカにしてるのかお?
![]() やらない夫
やらない夫
パーセプトロンによる学習はとてもシンプルでわかりやすいが、その分デメリットも大きい。
![]() やる夫
やる夫
えっ…。やらない夫は、いつも最後に残念な想いをさせるから、そういうのやめて欲しいお。終わり良ければ全て良しだお。
![]() やらない夫
やらない夫
最初に嫌な話をしても、それはそれでその後のモチベーションが下がるだろ。それに、デメリットを知っておくことは大事だぞ。
![]() やる夫
やる夫
そのデメリットによってやる夫の夢は打ち砕かれるのかお…
![]() やらない夫
やらない夫
パーセプトロンの最たるデメリットは線形分離可能な問題しか解けないということだ。
![]() やる夫
やる夫
線形分離可能?
![]() やらない夫
やらない夫
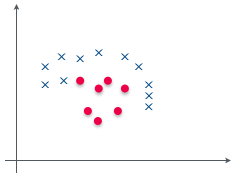
たとえば、こんな学習用データがあったとしよう。赤い点が 1 で、青いバツが -1 とするんだ。これを分類するために 1 本だけ直線を引くとしたら、やる夫はどんな風に線を引く?
![]() やる夫
やる夫
いや、こんなのどうやっても直線 1 本じゃ分類できないお。
![]() やらない夫
やらない夫
そうだ、この例のように直線 1 本では分類できないようなものは線形分離可能ではない。つまり、パーセプトロンでは分類できない。
![]() やる夫
やる夫
やる夫が作ろうとしている分類器も線形分離可能ではない、って言いたいのかお?
![]() やらない夫
やらない夫
画像を扱う場合、入力がかなりの高次元になるため可視化はできないが、顔の特徴を掴んで分類しようとするタスクはそんなに単純じゃない。確実に線形分離不可能だろうな。
![]() やる夫
やる夫
パーセプトロンなんて使い物にならんお。
![]() やらない夫
やらない夫
確かに、パーセプトロンは現場で使われることはほとんど無い。実際に解きたい問題が線形分離可能であることはほぼありえないからな。ほとんどが線形分離不可能な問題だ。でも安心しろ。ちゃんと実用的な分類器を構築するためのアルゴリズムもあるんだぞ。
![]() やる夫
やる夫
一旦落としておいて、その後に希望を見せるそのやり方、クセになるお。解決策があるって素晴らしいお。
![]() やらない夫
やらない夫
偉大な先人たちのおかげだな。
![]() やる夫
やる夫
ところで、やらない夫は大きいのと小さいのはどっちが好きなんだお?
![]() やらない夫
やらない夫
お前、ほんと好きだな、それ…