やる夫で学ぶ機械学習シリーズの第 3 回です。多項式回帰と重回帰について見ていきます。
第 2 回はこちら。やる夫で学ぶ機械学習 - 単回帰問題 -
目次はこちら。やる夫で学ぶ機械学習シリーズ
多項式回帰
やらない夫
さて、回帰の話にはもう少し続きがあるんだが。
やる夫
あんまり難しすぎるのは勘弁だお。
やらない夫
前回の延長だから、回帰が理解できていれば、そう難しい話ではないだろう。
やる夫
その前に、ちょっとおしっこいってくるお。
やらない夫
お前、そういうのは休憩中にやっとけよ…
やる夫
わかったお！仕方ないから我慢するお！！
やらない夫
意外と根性あるな…、ではこれから、前回の回帰の話をもう少し発展させていく。
やる夫
(あっ、ほんとに話を進めるのかお…)
やらない夫
前回、俺たちは、求めたい関数をこのように定義して、パラメータである $\theta$ を求めた。
$$ f_{\theta}(x) = \theta_0 + \theta_1 x $$
やる夫
覚えてるお。$f_{\theta}(x)$ を使った目的関数を定義して、最急降下法でパラメータの $\theta$ を求めたんだお。
やらない夫
$f_{\theta}(x)$ は一次関数だから、関数の形は当然のことながら直線になる。そこは大丈夫だよな。
やる夫
なんか回りくどいお。前回やったことはちゃんと覚えてるから、復習ならしなくていいお。
やらない夫
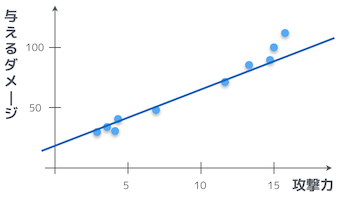
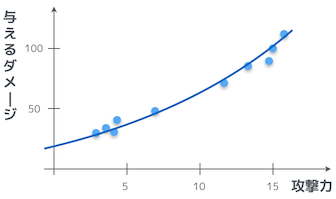
そうか。では、本題に入るが、最初に示したプロットは、実は直線より曲線の方がよりフィットするんだ。
やる夫
お、なるほど。確かに、曲線のグラフの方が、よりフィットしているように見えるお。
やらない夫
これは、関数 $f_\theta(x)$ を二次式として定義することで実現できる。
$$ f_{\theta}(x) = \theta_0 + \theta_1 x + \theta_2 x^2 $$
やらない夫
あるいは、それ以上の次数の式として定義すれば、より複雑な曲線にも対応できる。
$$ f_{\theta}(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3 + \cdots + \theta_n x^n $$
やる夫
どういう式にするのかは、勝手に自分で決めていいのかお？
やらない夫
そうだな、解きたい問題に対して、どの式が一番フィットするのかを見極めながら、いろいろ試してみる必要はあるがな。
やる夫
う、なんか面倒くさそうだお…
やらない夫
経験と勘がモノを言う部分だな。どれが最適なのかは、俺にもわからないからな。
やる夫
やらない夫にもわからないなら、仕方ないお…
やらない夫
さっきの二次式を見返してみると、新しいパラメータ $\theta_2$ が増えているな。このあと、どうすればいいかわかるか？
やる夫
ん、前と同じように偏微分して、パラメータ更新していけばいいのかお？こんな風に…
\begin{eqnarray}
\theta_0 & := & \theta_0 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)}) \
\theta_1 & := & \theta_1 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)})x^{(i)} \
\theta_2 & := & \theta_2 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)}){x^{(i)}}^2
\end{eqnarray}
やらない夫
そうだな。この式を使って $\theta_0, \theta_1, \theta_2$ を更新していけば、よりデータにフィットした $f_{\theta}(x)$ が得られる。当然だが、前にも言ったようにそれぞれの $\theta$ は同時に更新していく必要がある。
やる夫
これって、パラメータが $\theta_3, \theta_4, \cdots$ って増えていっても、同じことを繰り返せばいいのかお？
やらない夫
そういうことだ。こんな風に多項式の次数を増やした関数を使うものを多項式回帰と言うんだ。
やる夫
次数が高ければ高いほど、より正確に未知のデータを予測できる関数になるってことかお。
やらない夫
いや、そこはそうとも限らない。
やる夫
えっ、なんでだお…
やらない夫
過剰適合、またはオーバーフィッティング (Overfitting) と呼ばれる問題があってな。もちろん、オーバーフィッティングに対する解決策はある。が、それはまたの機会にとっておこう。
やる夫
もったいぶらないで説明してほしいお。
やらない夫
回帰の話にもう少し続きがあるから、先にそっちを説明したいんだ。それに、一度になんでもかんでも詰め込んでも、頭がパンクしてしまうぞ。
やる夫
そうかお…、やらない夫は言いくるめるのが上手だお。
やらない夫
言い方に悪意を感じるな、お前…
重回帰
やる夫
おしっこ行ってきたお。
やらない夫
多項式回帰の話の続き、いくぞ。
やる夫
よろしくお願いしますお。
やらない夫
今までは学習用データの変数は 1 つしかなった。
やる夫
学習用データの変数？攻撃力 $x$ のことかお？
やらない夫
そうだ。先の例では、攻撃力という 1 つの変数で、ダメージが決まっていた。ただ、実際は変数が 2 つ以上の複雑な問題なことが多い。
やる夫
さっきの多項式回帰で $x$ に加えて $x^2$ や $x^3$ を使う場合ってことかお。
やらない夫
いや、そうじゃない。確かに多項式回帰には別々の次数を持った複数の項があるが、実際に俺たちが使った変数は「攻撃力」のみだ。そうだろ？
やる夫
「攻撃力」と「攻撃力の 2 乗」と「攻撃力の 3 乗」の 3 つを使った、ってことじゃないのかお？
やらない夫
まあそうだが、本質的な変数は「攻撃力」のみだ。
やる夫
言ってることがよくわからんお。
やらない夫
今考えている問題設定を少し拡張するぞ。最初は、攻撃力が決まればダメージが決まる、という設定だったが、ダメージを決める要素は「攻撃力」の他に、実は「Lv」と「体力」という要素があるとしよう。
やる夫
あー、なるほど。変数が 2 つ以上って、そういうことかお。
やらない夫
そういうことだな。ところで、これまでは「変数」という言い方をしてきたが、機械学習の現場では「素性」と言ったりする。
やる夫
あぁ、なんか聞いたことがあるお。
やらない夫
素性が 1 つの時はグラフにプロットできたが、素性が 3 つとなると可視化することはできない。これからは図は省略することになるが…
やる夫
なんか先が思いやられる展開だお…
やらない夫
まぁ、これまでの話が理解できているのであれば大丈夫なはずだ。
やる夫
やらない夫の説明力を信じて、ついていくお…
やらない夫
今までは攻撃力を $x$ と置いていたが、これからは攻撃力を $x_1$、Lvを $x_2$、体力を $x_3$ と置くとすると、$f_{\theta}$ はどうなるかわかるか？
やる夫
ん、こんなんでいいのかお…？
$$ f_{\theta}(x_1, x_2, x_3) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 $$
やらない夫
正解だ。この時のパラメータ $\theta_0, \cdots, \theta_3$ を求めるにはどうすればいいかは、もうわかるな？
やる夫
目的関数を $\theta_0, \cdots, \theta_3$ についてそれぞれ偏微分して、パラメータを更新していけばいいお。
やらない夫
そうだな。では、実際のパラメータの更新式はどうなる？と聞きたいところだが、その前に式の表記をより簡単にしておこう。
やる夫
ん、どういうことかお？
やらない夫
素性が一般に $n$ 個ある場合のことを考えよう。$x_1, \cdots, x_n$ までの素性があるときの $f_{\theta}$ はどうなる？
やる夫
こうなるお。
$$ f_{\theta}(x_1, \cdots, x_n) = \theta_0 + \theta_1 x_1 + \cdots + \theta_n x_n $$
やらない夫
毎回そんな風に $n$ 個の $x$ を書いていくのは大変だから、パラメータ $\theta$ と素性 $x$ をベクトルとみなすんだ。
やる夫
ベクトルって、大きさと向きがある、矢印で表すアレかお？
やらない夫
それだな。まあ、今回は矢印というイメージは出てこないが…、むしろ列ベクトルだな。$\theta$ と $x$ をベクトルとして定義するとは、どういうことだと思う？
やる夫
んー、列ベクトルなんだったら、こういうことかお？
$$ \boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{array} \right] \ \ \ \boldsymbol{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] $$
やらない夫
おしいな。そのままだと、それぞれで次元が違うだろ。$\boldsymbol{\theta}$ は添字が 0 から始まるから $n+1$ 次元で、$\boldsymbol{x}$ の方は $n$ 次元だ。それだと扱いにくい。
やる夫
いや、そんなこと言われても、文字はもうこれだけしかないんだお…
やらない夫
何もベクトルの要素が全て文字じゃなくてもいい。こんな風に書きなおしてみよう。
$$ \boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{array} \right] \ \ \ \boldsymbol{x} = \left[ \begin{array}{c} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] $$
やる夫
勝手に 1 を足していいのかお？
やらない夫
むしろ、こうやって最初に 1 を置くほうが自然なんだ。$\boldsymbol{\theta}$ の方と合わせるために $x_0 = 1$ として、最初の要素に $x_0$ を置いてもいいな。
$$ \boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \end{array} \right] \ \ \ \boldsymbol{x} = \left[ \begin{array}{c} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] \ \ \ (x_0 = 1) $$
やらない夫
さて、ここで、$\boldsymbol{\theta}$ を転置したものと $\boldsymbol{x}$ を掛けてやると、どうなると思う？
やる夫
ん、ベクトルの各要素を掛けあわせて、それを全部足せばいいんだから、ちょっと面倒くさいけど、えっと…、こうかお。
$$ \boldsymbol{\theta}^{\rm{T}}\boldsymbol{x} = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n $$
やる夫
あ、$x_0 = 1$ だから、これって $f_{\theta}$ だお。
やらない夫
そういうことだ。つまり多項式で表していた $f_{\theta}$ は、ベクトルを使うと以下のように表せる。
$$ f_{\boldsymbol{\theta}}(\boldsymbol{x}) = \boldsymbol{\theta}^{\rm{T}}\boldsymbol{x} $$
やる夫
ずいぶんと簡潔になったお。
やらない夫
そして、$\boldsymbol{\theta}$ の $j$ 番目の要素を $\theta_j$ とすると、$E$ を $\theta_j$ で偏微分した時の式は、こんな風に書ける。ベクトルとスカラー値で、太字かそうでないかをちゃんと使い分けてるから、気をつけろよ。
$$ \frac{\partial E}{\partial \theta_j} = \sum_{i=1}^n (f_{\boldsymbol{\theta}} (\boldsymbol{x}^{(i)}) - y^{(i)}){x_j}^{(i)} $$
やる夫
なるほど。前から思ってたけど、やっぱりこの偏微分には規則性があったのかお。$j=0$ の時、つまり $\theta_0$ で偏微分する時も、後ろについてる $x_j$ は $x_0 = 1$ なので、結局は最初にやる夫が自分で微分した式と一致するお。
やらない夫
要するにパラメータの更新式は、こうだな。各 $\theta_j$ は同時更新する必要があるのは相変わらずだから気をつけろよ。
$$ \theta_j := \theta_j - \eta\sum_{i=1}^n (f_{\boldsymbol{\theta}} (\boldsymbol{x}^{(i)}) - y^{(i)}){x_j}^{(i)} $$
やる夫
ミッション・コンプリートだお！！
やらない夫
な、今までの話が理解できていれば、素性が増えたとしても大したことは無いだろう。
やる夫
やる夫が優秀だからだお。
やらない夫
突然どこから出てくるんだよ、その自信。こんな風に素性を 2 つ以上使ったものを重回帰と言うんだ。逆に、最初にやった例のように素性が 1 つの場合は、単回帰と言うな。
やる夫
単回帰に、多項式回帰に、重回帰。覚えたお。
やらない夫
回帰の話はこの辺で終わりだな。
やる夫
最後のベクトル化から続く怒涛の一般化ラッシュ、気持よかったお。
やらない夫
一般化して考えられるのは、数学のいいところだな。
やる夫
ところで、これまでやってきた最急降下法、パラメータの更新にシグマが含まれてるから、全学習データ分だけループすることになるんだお。学習用データが大量にあった場合、for ループの回数が増えて、時間がかかってしまわないかお？
やらない夫
さすがプログラミングが得意なだけあって、効率云々を気にするんだな。そうだ、やる夫の言うとおり、計算量が多くて遅いことが最急降下法の欠点の 1 つだ。
やる夫
まあ、性能の良いマシンを買えば解決するかお。
やらない夫
金に物を言わせるなよ…、そこはプログラマっぽくないな、お前。ちゃんと、もっと速いアルゴリズムがあるんだよ。むしろ、最急降下法よりも、そっちの速いアルゴリズムの方が好んで使われるな。
やる夫
じゃ、最初からそっちの速いアルゴリズムの方を教えてくれればよかったお…
やらない夫
速いアルゴリズムの方は最急降下法をベースにしてるんだよ。先に速いアルゴリズムを説明しても、どうせ最急降下法から説明することになるんだから、結局は同じことだ。それに、こういうことは基礎からちゃんとやっといたほうが、後で応用が聞くんだぞ？
やる夫
うっ、やっぱりやらない夫には言いくるめられてしまうお…
やらない夫
お前、言い方…
確率的勾配降下法
やらない夫
最後に確率的勾配降下法というアルゴリズムを見ていこう。
やる夫
それが、さっき言った速いアルゴリズムのことかお？
やらない夫
そうだな。最急降下法には、さっきやる夫がいった計算に時間がかかること以外にも、収束が遅かったり、それから局所解に捕まってしまう、というデメリットもある。
やる夫
局所解につかまるって、どういうことかお？
やらない夫
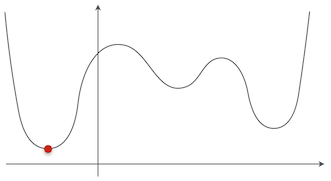
最急降下法を説明する時に使った関数の例は $g(x) = (x - 1)^2$ という二次関数だったから問題なかったが、もっと複雑な形の関数を考えてみよう。この関数の最小値は、赤い点で示してある位置だな。
やる夫
ぐにゃぐにゃしてるグラフだお…
やらない夫
最急降下法で関数の最小値を見つけるにしても、まず最初に初期値を決める必要がある。
やる夫
あー、確かにやったお。例の時は $x = 3$ からはじめたお。あれは、なんで 3 からスタートさせたのかお？
やらない夫
俺が適当に選んだ値だ。
やる夫
やらない夫神に導かれるままについていきますお。
やらない夫
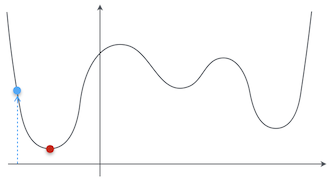
そうじゃなくて、初期値は適当に決めていいって意味だ。ただ、そのせいで局所解に捕まるという問題が発生するんだ。たとえば、この図の青い点が初期値だったとしたら、どうだ？
やる夫
あー、なんとなくわかってきたお。その青い点が初期値だったら、最急降下法でちゃんと赤い点の最小値が求まるお。
やらない夫
では、赤い点の最小値が求まらないのは、どういう場合だ？
やる夫
たとえば、今度はこっちの青い点が初期値だった場合、赤い点まで移動せずに、たぶんオレンジの点で止まってしまうお。
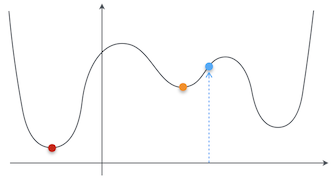
やらない夫
それが局所解に捕まるということだ。
やる夫
アルゴリズムがシンプルな分、いろいろな問題があるってことかお。
やらない夫
そこで、そういった最急降下法のデメリットを克服したアルゴリズムが、確率的勾配降下法だ。
やる夫
ふむ。具体的にはどういうアルゴリズムなんだお？
やらない夫
最急降下法のパラメータ更新の式は覚えてるか？
やる夫
覚えてるお。
$$ \theta_j := \theta_j - \eta\sum_{i=1}^n (f_{\boldsymbol{\theta}} (\boldsymbol{x}^{(i)}) - y^{(i)}){x_j}^{(i)} $$
やらない夫
よし。その式では、パラメータの更新に全ての学習用データの誤差を使っているが、確率的勾配降下法ではランダムに学習用データを 1 つ選んで、それをパラメータの更新に使うんだ。式中の $k$ は、パラメータ更新毎にランダムに選ばれたインデックスだ。
$$ \theta_j := \theta_j - \eta(f_{\boldsymbol{\theta}} (\boldsymbol{x}^{(k)}) - y^{(k)}){x_j}^{(k)} $$
やる夫
お、シグマがなくなってるお。
やらない夫
そうだな。最急降下法で 1 回パラメータを更新する間に、確率的勾配降下法では $n$ 回パラメータを更新できる。また、学習用データをランダムに選んで、その時点での勾配でパラメータを更新していくので、目的関数の局所解に捕まりにくい。
やる夫
そんなに適当なやり方で、ちゃんとした答えが得られるのかお？
やらない夫
この方法でも、実際に最適解に収束するということがわかっている。
やる夫
うーん、なんか不思議だお。
やらない夫
もちろん、学習率 $\eta$ を適切に設定することは大事だ。特に、学習する度に $\eta$ を小さくしていく、という手法も存在する。
やる夫
そうだ、最急降下法の時も思ってたけど、$\eta$ の適切な値って、どうやって見つければいいのかお？
やらない夫
難しい問題だな。解決のためのアイデアは、興味があれば探してみるといい。
やる夫
やらない夫、実は知らないのかお。
やらない夫
これ以上続けると、話が長くなりすぎるからな。
やる夫
あっ、はぐらかしたお。読者のことを考えてるふりをするなんて、ずるいお。
やらない夫
まあ、そういうところは、実際に実装しはじめて困ったときに探すので十分だ。やり始める前から、なんでもかんでも一気に詰め込むのはよくないぞ。
やる夫
はいはいですお。
