やる夫で学ぶ機械学習シリーズの第 6 回です。ロジスティック回帰の目的関数である尤度関数をもう少し詳しくみて、線形分離不可能な問題にどのように適用していくのかを見ていきます。

第 5 回はこちら。やる夫で学ぶ機械学習 - ロジスティック回帰 -

目次はこちら。やる夫で学ぶ機械学習シリーズ

対数尤度関数

やらない夫
尤度関数を微分してパラメータ $\boldsymbol{\theta}$ の更新式を求めてみようか。

やる夫
もう脳みそパンパンですお。

やらない夫
その前に、尤度関数はそのままだと扱いにくいから、少し変形しよう。

やる夫
扱いにくい？どういうことかお？

やらない夫
まず同時確率という点だ。確率なので 1 以下の数の掛け算の連続になることはわかるな？

やる夫
確かに、確率の値としては 0 より大きくて 1 より小さいものだお。

やらない夫
1 より小さい数を何度も掛け算すると、どんどん値が小さくなっていくだろう。コンピュータで計算する場合はそれは致命的な問題だ。

やる夫
あー、オーバーフローの逆かお。アンダーフロー。

やらない夫
次に掛け算という点だ。掛け算は足し算に比べて計算が面倒だ。

やる夫
小数点の計算とかあんまりやりたくないお。

やらない夫
そこで一般的には尤度関数の対数をとったもの、対数尤度関数を使う。

$$ \log L(\boldsymbol{\theta}) = \log \prod_{i=1}^n P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}} $$

やる夫
目的関数に対して勝手に対数をとったりして、答え変わらないのかお？

やらない夫
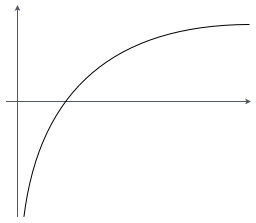
問題ない。対数関数は単調増加な関数だからだ。対数関数のグラフの形を覚えているか？

やる夫
確かこんな感じのグラフだお。

やらない夫
それで正解だ。グラフがずっと右上がりになってることがわかるだろう。つまり単調増加な関数ってのは $x_1 < x_2$ ならば $f(x_1) < f(x_2)$ となるような関数 $f(x)$ だということだ。

やる夫
なるほど、確かに $\log(x)$ はそういう風になっているお。

やらない夫
$\log$ は単調増加関数だから、今考えいてる対数尤度関数についても $L(\boldsymbol{\theta_1}) < L(\boldsymbol{\theta_2})$ であれば $\log L(\boldsymbol{\theta_1}) < \log L(\boldsymbol{\theta_2})$ ということが言えるだろう。要するに $L(\boldsymbol{\theta})$ を最大化することと $\log L(\boldsymbol{\theta})$ を最大化することは同じことなんだ。

やる夫
ふーん、よく考えられてるお。

やらない夫
では、対数尤度関数を少し変形して $f_{\boldsymbol{\theta}}$ を使って表してみよう。

$$ \begin{eqnarray} \log L(\boldsymbol{\theta}) & = & \log \prod_{i=1}^n P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}} \
& = & \sum_{i=1}^n \left( \log P(y^{(i)}=1|\boldsymbol{x})^{y^{(i)}} + \log P(y^{(i)}=0|\boldsymbol{x})^{1-y^{(i)}} \right) \
& = & \sum_{i=1}^n \left( y^{(i)} \log P(y^{(i)}=1|\boldsymbol{x}) + (1-y^{(i)}) \log P(y^{(i)}=0|\boldsymbol{x}) \right) \
& = & \sum_{i=1}^n \left( y^{(i)} \log f_{\boldsymbol{\theta}}(\boldsymbol{x}) + (1-y^{(i)}) \log (1-f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) \end{eqnarray} $$

やる夫
うっ、ちょっと式変形を追うのが大変だお…

やらない夫
実際には 2 行目は $\log(ab) = \log a + \log b$ という性質を、3 行目は $\log a^b = b \log a$ という性質を使っているだけだ。

やる夫
$\log$ の性質は覚えてるけど、最後の行はなんでそうなるんだお。

やらない夫
確率の定義からだ。ここでは確率変数の取る値としては $y=1$ か $y=0$ かしかないから、$P(y^{(i)}=1|\boldsymbol{x}) = f_{\boldsymbol{\theta}}(\boldsymbol{x})$ ならば $P(y^{(i)}=0|\boldsymbol{x}) = 1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})$ となる。

やる夫
あー、そうか。全部の確率を足すと 1 になるんだったお。

やらない夫
ここまでで俺たちは目的関数として対数尤度関数 $\log L(\boldsymbol{\theta})$ を定義した。次はどうする？

やる夫
$\log L(\boldsymbol{\theta})$ を $\boldsymbol{\theta}$ の各要素 $\theta_j$ で微分…かお？

やらない夫
ではこれを微分していこう。

$$ \frac{\partial}{\partial \theta_j} \sum_{i=1}^n \left( y^{(i)} \log f_{\boldsymbol{\theta}}(\boldsymbol{x}) + (1-y^{(i)}) \log (1-f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) $$

やる夫
ちょっと何言ってるかよくわからん式だお…

やらない夫
回帰の時にやったように、合成関数の微分を使うんだ。

やる夫
えーと、要するに…こうかお？

$$ \frac{\partial \log L(\boldsymbol{\theta})}{\partial f_{\boldsymbol{\theta}}} \cdot \frac{\partial f_{\boldsymbol{\theta}}}{\partial \theta_j} $$

やらない夫
それでいい。ひとつずつ微分していくんだ。まず第一項はどうなるだろう？

やる夫
第一項は $\log L(\boldsymbol{\theta})$ を $f_{\boldsymbol{\theta}}$ で微分するんだから…えーっと、$\log(x)$ の微分は $\frac{1}{x}$ でよかったかお？

$$ \begin{eqnarray} \frac{\partial \log L(\boldsymbol{\theta})}{\partial f_{\boldsymbol{\theta}}} & = & \frac{\partial}{\partial f_{\boldsymbol{\theta}}}\sum_{i=1}^n \left( y^{(i)} \log f_{\boldsymbol{\theta}}(\boldsymbol{x}) + (1-y^{(i)}) \log (1-f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) \
& = & \sum_{i=1}^n \left( \frac{y^{(i)}}{f_{\boldsymbol{\theta}}(\boldsymbol{x})} - \frac{1-y^{(i)}}{1-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \right) \
\end{eqnarray} $$

やる夫
一気に第二項もやってしまうお。これも合成関数の微分を使うお。$z = 1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})$ と置いて $f_{\boldsymbol{\theta}}(\boldsymbol{x}) = z^{-1}$ とすると

$$ \begin{eqnarray} \frac{\partial f_{\boldsymbol{\theta}}}{\partial \theta_j} & = & \frac{\partial f_{\boldsymbol{\theta}}}{\partial z} \cdot \frac{\partial z}{\partial \theta_j} \
& = & -\frac{1}{z^2} \cdot -x_j \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x}) \
& = & \frac{x_j \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{(1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}))^2} \end{eqnarray} $$

やる夫
できたお！これが微分結果だお。

$$ \frac{\partial \log L(\boldsymbol{\theta})}{\partial \theta_j} = \sum_{i=1}^n \left( \frac{y^{(i)}}{f_{\boldsymbol{\theta}}(\boldsymbol{x})} - \frac{1-y^{(i)}}{1-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \right) \frac{x_j \exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{(1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}))^2} $$

やらない夫
そうだ、と言いたいところだが、ただ計算すればいいってもんじゃないだろ…やる夫はこれを見てどう思う？

やる夫
どう思うも何も、これでパラメータの更新式ができるお…まあ、二度と見たくもないような複雑な式ですお。

やらない夫
そう、実はまだ複雑なんだ。もう少し式変形を進めて綺麗な形にできるんだが…

やる夫
やる夫の計算力が足りないってことかお！

やらない夫
いや、ここまでできただけでも十分だ。一緒に考えよう。まず、後ろの方の $\exp$ が含まれている式の方を見てみようか。やる夫は全部まとめているが、そこをあえてこんな風に分けてみよう。

$$ \frac{x_j \exp(\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{(1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}))^2} = \frac{1}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot \frac{\exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot x_j $$

やる夫
えっ、わざわざ分解するのかお。

やらない夫
そうするとこういう風に $f_{\boldsymbol{\theta}}(\boldsymbol{x})$ を使って書けるだろう。

$$ \frac{1}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot \frac{\exp(-\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x})}{1 + \exp(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x})} \cdot x_j = f_{\boldsymbol{\theta}}(\boldsymbol{x}) \cdot (1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})) \cdot x_j $$

やる夫
あーなるほど。確かにやらない夫の言う通りに変形できそうだお。でも、第二項が $1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})$ になるのはわかるけど、そんなの気付けないお…

やらない夫
式を変形する作業は慣れの問題も大きいだろうから、できなかったといってヘコむことはない。ちなみにシグモイド関数、ここでは $\sigma(x)$ と置こう、これの微分が $\sigma(x)(1-\sigma(x))$ になるのは有名だな。

やる夫
確かに $f_{\boldsymbol{\theta}}$ はシグモイド関数で、それを微分した形はそうなってるお。

やらない夫
では、この式を微分結果に代入してみよう。約分した後に展開して整理すると最終的にはこんな形になる。

$$ \begin{eqnarray} \frac{\partial \log L(\boldsymbol{\theta})}{\partial \theta_j} & = & \sum_{i=1}^n \left( \frac{y^{(i)}}{f_{\boldsymbol{\theta}}(\boldsymbol{x})} - \frac{1-y^{(i)}}{1-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \right) f_{\boldsymbol{\theta}}(\boldsymbol{x}) (1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})) x_j \
& = & \sum_{i=1}^n \left( y^{(i)}(1 - f_{\boldsymbol{\theta}}(\boldsymbol{x})) - (1-y^{(i)})f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) x_j \
& = & \sum_{i=1}^n \left(y^{(i)} - f_{\boldsymbol{\theta}}(\boldsymbol{x}) \right) x_j \end{eqnarray} $$

やる夫
めちゃくちゃ単純な式になったお…やらない夫すごすぎるお。

やらない夫
あとはいつものように、この式からパラメータ更新式を導出するんだ。ただし、回帰の時は最小化すればよかったが、今回は最大化なので注意が必要だ。そこが違うので、ただ代入すればいいというわけじゃない。

やる夫
あ、確かにそうだお…もうすぐ終わりそうなのに、ここにきてまた壁がでてきたお。

やらない夫
そう難しく考えるな。最大化問題を最小化問題に置き換える簡単な方法がある。符号を反転させればいいだけだ。

やる夫
まじかお？

やらない夫
単純だろう。$f(x)$ を最大化させる問題と、その符号を反転させた $-f(x)$ を最小化させる問題はまったく同じ問題だ。

やる夫
希望が見えてきたお。要するにこれまでは $\log L(\boldsymbol{\theta})$ を最大化することを考えてきたけど、これからは $-\log L(\boldsymbol{\theta})$ を最小化することを考えればいいってことかお？

やらない夫
その通りだ。符号が反転したんだから、微分結果の符号も反転する。$L^{-}(\boldsymbol{\theta}) = -\log L(\boldsymbol{\theta})$ と置くと、こうなるな。

$$ \frac{\partial L^{-}(\boldsymbol{\theta})}{\partial \theta_j} = \sum_{i=1}^n \left(f_{\boldsymbol{\theta}}(\boldsymbol{x}) - y^{(i)} \right) x_j $$

やる夫
てことは、パラメータ更新式は、こうかお？

$$ \theta_j := \theta_j - \eta \sum_{i=1}^n \left(f_{\boldsymbol{\theta}}(\boldsymbol{x}) - y^{(i)} \right) x_j $$

やらない夫
よし、できたな。

線形分離不可能問題

やらない夫
では、いよいよ線形分離不可能な問題にも挑戦していこうか。

やる夫
待ってましたお。

やらない夫
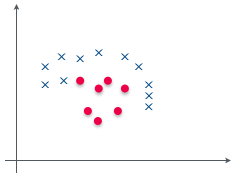
これが線形分離不可能だということはもういいな？

やる夫
わかってるお。

やらない夫
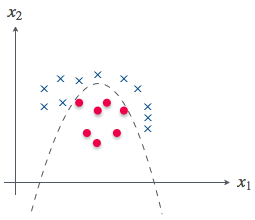
線形分離不可能な問題は、すなわち直線では分離できないということだ。であれば、曲線で分離すればいいという発想に自然といきつく。

やる夫
お、もしかして多項式回帰の時にやったように、次数を増やしてみるってことかお？

やらない夫
勘がいいな。よし、これは 2 次元の話なので、素性としては $x_1$ と $x_2$ の 2 つがある。そこに 3 つ目の素性として $x_1^2$ を加える事を考えて見るんだ。

やる夫
こういうことかお？

$$ \boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \
\theta_1 \
\theta_2 \
\theta_3 \end{array} \right] \ \ \ \boldsymbol{x} = \left[ \begin{array}{c} 1 \
x_1 \
x_2 \
x_1^2 \end{array} \right] $$

やらない夫
そうだな。つまり $\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x}$ はこうだ。大丈夫か？

$$ \boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 $$

やる夫
わかるお。

やらない夫
また適当に $\boldsymbol{\theta}$ を決めてみよう。そうだな、たとえば $\boldsymbol{\theta}$ がこうなった時、それぞれ $y=1$ と $y=0$ と分類される領域はどこになる？

$$ \boldsymbol{\theta} = \left[ \begin{array}{c} \theta_0 \
\theta_1 \
\theta_2 \
\theta_3 \end{array} \right] = \left[ \begin{array}{c} 0 \
0 \
1 \
-1 \end{array} \right] $$

やる夫
えーっと、要するに $\boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x} \ge 0$ を考えればいいんだから…前と同じように変形してみるお。

$$ \begin{eqnarray} \boldsymbol{\theta}^{\mathrm{T}}\boldsymbol{x} = x_2 - x_1^2 & \ge & 0 \
x_2 & \ge & x_1^2 \end{eqnarray} $$

やる夫
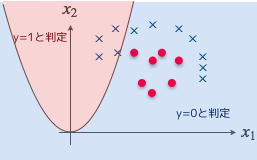
こんな感じかお？

やらない夫
その通りだ。以前は決定境界が直線だったが、今は曲線になっているのが見て取れるだろう。

やる夫
見た感じ、この決定境界だとまったく分類できてないように見えるけど、それはいつものようにやらない夫神が適当に $\boldsymbol{\theta}$ を決めたから、ってことでいいかお？

やらない夫
もう慣れてきたようだな。やる夫の言う通りだ。

やる夫
じゃ、これをさっき求めたパラメータ更新式を使って、$\boldsymbol{\theta}$ を学習していけばいいってことかお。

やらない夫
これで線形分離不可能な問題も解けるようになったな。

やる夫
楽勝だお！

やらない夫
あとは、好きなように次数を増やせば複雑な形の決定境界にすることができる。たとえばさっきは素性として $x_1^2$ を増やしたが $x_2^2$ も増やすと、円状の決定境界ができる。

やる夫
ロジスティック回帰のパラメータ更新って、最初に回帰で考えた時と同じように全データで学習してるけど、ここにも確率的勾配降下法って使えるのかお？

やらない夫
もちろん使えるぞ。

やる夫
ロジスティック回帰って万能だお。

やらない夫
やる夫はいつも結論を出すのが早すぎだな。どんな問題に対しても万能なアルゴリズムなんて存在しないんだから適材適所で使っていかなければならない。

やる夫
今のやる夫はまだパーセプトロンとロジスティック回帰しか知らないんだから、ロジスティック回帰の方がやる夫にとっては有能な分類アルゴリズムだお。

やらない夫
それもそうだな。分類器はいろいろなアルゴリズムがあるから、勉強していくと楽しいぞ。

やる夫
自習なんて面倒くさいお…

やらない夫
本当に面倒くさがりなんだな、お前…

やる夫
天性だお。

やらない夫
自慢するところかよ。しかしこれまでだいぶ理論を説明してきたが、理論だけじゃなくて実際になにか作ってみることも大事だ。理解度が飛躍的に上がるぞ。

やる夫
じゃ、やっぱり前に言ってたアレ、作るお…

やらない夫
その熱意には負けるよ。

やる夫で学ぶ機械学習 - 過学習 - へ続く。