やる夫で学ぶ機械学習シリーズの第 2 回です。回帰について見ていきます。
第 1 回はこちら。やる夫で学ぶ機械学習 - 序章 -
目次はこちら。やる夫で学ぶ機械学習シリーズ
問題設定
![]() やらない夫
やらない夫
今日は回帰について詳しく見ていく。
![]() やる夫
やる夫
回帰って響きがカッコいいお。
![]() やらない夫
やらない夫
ここからは、より具体的な例を混じえながら話を進めていこう。
![]() やる夫
やる夫
具体例は、やる夫の明日のお昼ごはんぐらい大事だお。
![]() やらない夫
やらない夫
まったく意味がわからないたとえなんだが…。そうだな、たとえば、主人公の攻撃力によって、敵キャラに与えるダメージが決まるゲームがあるとしよう。
![]() やる夫
やる夫
よくある設定だお。
![]() やらない夫
やらない夫
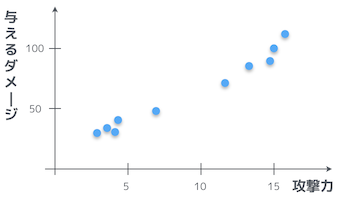
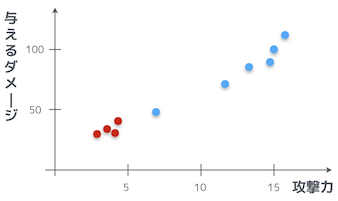
ダメージには揺らぎがあって、常に同じダメージを与えられるとは限らない。さて、実際に何度か敵キャラに攻撃してみて、その時の攻撃力と与えたダメージをグラフにプロットしてみると、こんな風になっていたとしよう。
![]() やる夫
やる夫
なるほど。攻撃力が高くなればなるほど、与えるダメージも大きくなっているお。
![]() やらない夫
やらない夫
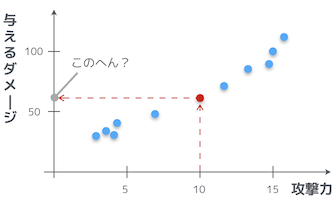
やる夫はコレを見て、攻撃力が 10 の時にどれくらいダメージを与えられるかわかるか?
![]() やる夫
やる夫
馬鹿にしてるのかお!そんなの簡単だお。だいたい 60 前後くらいだお?
![]() やらない夫
やらない夫
そうだな。俺たちはこれから機械学習を使って、今やる夫がやったように、攻撃力からダメージを予測していく。
![]() やる夫
やる夫
そんなの、このプロットを見れば、だいたい誰にでもわかるお?
![]() やらない夫
やらない夫
それはこの問題設定が単純だからだよ。実際に機械学習を使って解きたい問題は、複雑な問題であることがほとんだ。そういうものを機械にまかせるために、データから学習させるんだよ。それが機械学習だ。後からもっと複雑な問題も見ていくから、その時もまた同じことが言えるかどうかだな。
![]() やる夫
やる夫
ふーん。
最小二乗法
![]() やる夫
やる夫
どうやって学習していくんだお?
![]() やらない夫
やらない夫
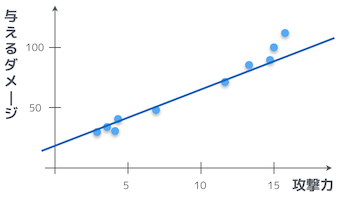
関数をイメージするんだ。このプロットの各点を通る関数の形がわかれば、攻撃力からダメージがわかるだろ。ただし、ダメージにはノイズが含まれているから、関数がきっちり全ての点を通るわけじゃない。
![]() やる夫
やる夫
これは一次関数だお!一次関数は、切片と傾きがわかれば関数の形が決まるから、それを調べることになるのかお?
![]() やらない夫
やらない夫
冴えてるな。俺たちがいまから考える関数は、切片と傾きを $\theta$ を使って表すと、こんな風になる。
$$ y = \theta_0 + \theta_1 x $$
![]() やる夫
やる夫
うっ、式が出てくると急に数学っぽくなるお…、$\theta$ ってなんだお。
![]() やらない夫
やらない夫
$\theta$ はこれから俺たちが求めていく未知数だ。パラメータとも言う。文字は別になんでもいいんだが、統計学の世界では、未知数や推定値を $\theta$ で表すことが多いので、今回も $\theta$ を使っただけだ。
![]() やる夫
やる夫
まあ、今の例の場合は切片と傾きだと思っておくお。
![]() やらない夫
やらない夫
今はそれで問題ないだろう。そして、わかっているとは思うが $x$ が攻撃力、$y$ がダメージに対応している。
![]() やる夫
やる夫
そこは OK だお。
![]() やらない夫
やらない夫
なにか具体的な値を実際に代入して確認してみるとイメージもつきやすいだろう。そうだな、たとえば $\theta_0 = 1$、$\theta_1 = 2$ としてみよう。さっきの式はどうなるかわかるか?
![]() やる夫
やる夫
やらない夫の質問はいつも優しすぎるお。代入するだけだお。
$$ y = 1 + 2x $$
![]() やらない夫
やらない夫
よし、ではその式の $x$ に何か代入して $y$ を求めてみようか。
![]() やる夫
やる夫
$x = 5$ の時を計算してみるお。
\begin{eqnarray}
y & = & 1 + 2x \
& = & 1 + 2 \cdot 5 \
& = & 11
\end{eqnarray}
![]() やらない夫
やらない夫
つまり、パラメータが $\theta_0 = 1$、$\theta_1 = 2$ の場合は、攻撃力が 5 の時に与えるダメージは 11 くらいになるってことだ。
![]() やる夫
やる夫
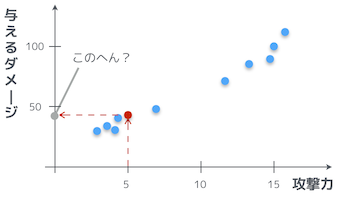
でも、さっきのグラフを見ると攻撃力 5 の時は、だいたい 40 〜 50 くらいはダメージを与えてるお。
![]() やらない夫
やらない夫
そうだな。つまり俺たちがいま適当に定義したパラメータは間違ってるってことだ。これから、機械学習を使って、この $\theta_0$ と $\theta_1$ の正しい値を求めていくんだ。
![]() やる夫
やる夫
把握したお。で、どうやって求めていくんだお?
![]() やらない夫
やらない夫
その前に、さっきの式をこのように書き直すぞ。
$$ f_{\theta}(x) = \theta_0 + \theta_1 x $$
![]() やる夫
やる夫
$y$ が $f_{\theta}(x)$ に変わっただけだお。てか、なんでこんなことするお?
![]() やらない夫
やらない夫
こうすることによって、これが $\theta$ というパラメータを持ち、$x$ という変数の関数だということを明示的に表せるだろう。それに $y$ のままにしておくと、この後に混乱することになるからな。
![]() やる夫
やる夫
ふーん。まあ、やらない夫がそうするっていうなら、だまって従うお。
![]() やらない夫
やらない夫
肝心の $\theta$ の求め方だが、いま、俺たちの手元には、攻撃力とダメージのデータがある。さっきのグラフにプロットしてあった点だな。つまり学習用のデータだ。これを $f_{\theta}(x)$ に代入して得られた値と、実際の値の差が最小になるように $\theta$ を決定していくんだ。
![]() やる夫
やる夫
ん、ちょっと何いってるかよくわからないお…
![]() やらない夫
やらない夫
具体的にいくつか学習用データを列挙してみよう。攻撃力に小数点があるのはいささか奇妙だが、とりあえず違和感は置いておこう。
| 攻撃力($x$) | ダメージ($y$) |
|---|---|
| 3.0 | 30 |
| 3.7 | 35 |
| 4.3 | 33 |
| 4.6 | 44 |
![]() やる夫
やる夫
やらない夫は、この 4 つの赤い点のデータを列挙したのかお?
![]() やらない夫
やらない夫
そうだ。さっき、パラメータを $\theta_0 = 1$、$\theta_1 = 2$ という風に適当に決めて、$1 + 2x$ という式を作ったが、これに実際に $x$ の値を代入したものを表に足してみるぞ。
| 攻撃力($x$) | ダメージ($y$) | $\theta_0 = 1$、$\theta_1 = 2$ の時の $f_{\theta}(x)$ |
|---|---|---|
| 3.0 | 30 | 7.0 |
| 3.7 | 35 | 8.4 |
| 4.3 | 33 | 9.6 |
| 4.6 | 44 | 10.2 |
![]() やらない夫
やらない夫
これを見て、学習用データの値、つまり $y$ だな、それと $f_{\theta}(x)$ で計算した値が、ズレてることがわかるか?
![]() やる夫
やる夫
かなりズレてるお。
![]() やらない夫
やらない夫
ただ、$y$ と $f_{\theta}(x)$ の値は一致しているのが理想だ。わかるか?
![]() やる夫
やる夫
わかるお。$y$ を予測するための関数が $f_{\theta}(x)$ なんだお。
![]() やらない夫
やらない夫
理想に近づけるためには $y$ と $f_{\theta}(x)$ の誤差、つまり $|y - f_{\theta}(x)|$ が小さくなれば良い。全ての学習用データにおいて、誤差の和が最も小さくなるようなパラメータ $\theta$ を見つければいいというわけだ。こういう問題は最適化問題と呼ばれる。ついてこれてるか?
![]() やる夫
やる夫
うっ、うん、なんとか…
![]() やらない夫
やらない夫
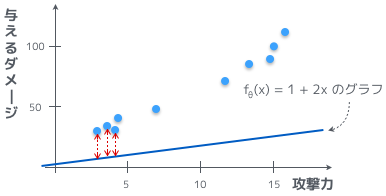
図を使うと、よりわかりやすいかもしれないな。青い点が学習用データ、青い線が $1 + 2x$ のグラフ、そして赤い点線がそれらの差だ。
![]() やる夫
やる夫
あ、これだとわかりやすいお。誤差を最小にするってことは、この赤い点線の高さを小さくするってことだお。それはつまり、$f_{\theta}(x)$ が学習用のデータにフィットしていくってことになるお。
![]() やらない夫
やらない夫
そういうことだな。学習用データの個数を n 個とすると、誤差の和は以下のような式で表せる。この式では $\theta$ が変数となっているところに注意だ。
$$ E(\theta) = \frac{1}{2}\sum_{i=1}^n (y^{(i)} - f_{\theta} (x^{(i)}))^2 $$
![]() やる夫
やる夫
いや、いきなり難易度あげすぎだお。まだ心の準備ができてなかったお。
![]() やらない夫
やらない夫
まず、誤解されないように最初に説明しておくと、$x^{(i)}$ や $y^{(i)}$ は i 乗という意味ではなくて、i 番目の学習用データということだ。$x^{(1)}$ は 3.0 で $y^{(1)}$ が 30、それから $x^{(2)}$ は 3.7 で $y^{(2)}$ が 35、という具合だな。
![]() やる夫
やる夫
そこは、なんとなくそういう雰囲気を感じていたお。
![]() やらない夫
やらない夫
誤差の部分だが、実際には単純な誤差じゃなくて二乗誤差を使っている。なので、誤差の部分を二乗しているんだ。
![]() やる夫
やる夫
全体を 2 で割ってるのは何だお?
![]() やらない夫
やらない夫
後で $E(\theta)$ を微分することになるんだが、微分した式をちょっとだけ簡単にするためのトリックだ。最適化問題は、何か定数が全体に掛かっていたとしても、求まる答えは変わらないからこういうことができる。まあ、あまり深く考えなくていいさ。
![]() やる夫
やる夫
おまじない的なものは気持ち悪いお…、うーん、全体像はわかったけど、ちょっと、まだピンときてないお。
![]() やらない夫
やらない夫
具体的に値を入れて計算してみるか。$\theta_0 = 1$、$\theta_1 = 2$ として、さっき列挙した 4 つの学習用データを実際に代入してみよう。$f_\theta(x^{(i)})$ や $y^{(i)}$ はさっきの表の値を参照すると…
\begin{eqnarray}
E(\theta) & = & \frac{1}{2}\sum_{i=1}^n (y^{(i)} - f_{\theta} (x^{(i)}))^2 \
& = & \frac{1}{2}\left((30 - 7.0)^2 + (35 - 8.4)^2 + (33 - 9.6)^2 + (44 - 10.2)^2\right) \
\
& = & \frac{529.0 + 707.5 + 547.5 + 1142.4}{2} \
& = & 1463.2
\end{eqnarray}
![]() やる夫
やる夫
1463.2?
![]() やらない夫
やらない夫
この 1463.2 という値自体に特に意味はないが、この値がどんどん小さくなるように、パラメータの $\theta$ を更新していくことが目的だ。
![]() やる夫
やる夫
あー、この値が小さくなるということは、つまり予測値 $f_\theta(x)$ と、学習用データ $y$ の誤差が小さくなる、ということかお。
![]() やらない夫
やらない夫
そういうことだ。このようなアプローチは最小二乗法と呼ばれる。
最急降下法
![]() やる夫
やる夫
$E(\theta)$ の値を小さくしたいのはわかったけど、どうやって小さくしていくんだお?$\theta$ を適当に決めて、値を代入して、前の値と比較していくのはさすがに面倒だお。
![]() やらない夫
やらない夫
そんな面倒なことはしないさ。この $E(\theta)$ のことを「目的関数」や「コスト関数」と呼ぶんだが、これを $\theta_0$ と $\theta_1$ について偏微分していく。
![]() やる夫
やる夫
偏微分?そんなもんで、わかるのかお?
![]() やらない夫
やらない夫
微分の定義を思い出せ。微分は変化の度合いを求めるためのものだったろう。微分を習った時に、増減表を作ったりしなかったか?
![]() やる夫
やる夫
増減表…、そういえば、そんなものがあったお。なつかしいお。
![]() やらない夫
やらない夫
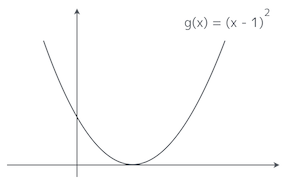
簡単な例で試してみようか。こういう二次関数があるとしよう。最小値は明らかに $x = 1$ の時の $g(1) = 0$ だな。この二次関数の増減表はどうなる?
![]() やる夫
やる夫
お…、今回の質問は少し難易度があがったお。えーっと…、まずは関数を微分するお。
$$ \frac{d}{dx}g(x) = 2x - 2 $$
![]() やる夫
やる夫
んで、導関数の符号を見ながら、増減表を作って…、これでいいかお?
| $x$ の範囲 | $x < 1$ | $x = 1$ | $x > 1$ |
|---|---|---|---|
| $\frac{d}{dx}g(x)$ の符号 | - | 0 | + |
| $g(x)$ の増減 | ↘ | ↗ |
![]() やらない夫
やらない夫
よし。この増減表を見ると、$x < 1$ の時は右下がりになっている。逆に $x > 1$ の時は右上がり、これは言い換えると左下がりになっているな。
![]() やる夫
やる夫
増減表を見ても、グラフを見ても、確かにそうなっているお。
![]() やらない夫
やらない夫
たとえば $x = 3$ からスタートして $g(x)$ の値を小さくするためには、$x$ を少しずつ左にずらしていけばいい。なぜなら、増減表から $x > 1$ の時は、グラフが左下がりになっているのがわかるからだ。$x = -3$ からだと、逆に右にずらしていけばいいな。
![]() やる夫
やる夫
それって、導関数の符号によって、$x$ をずらす方向が変わるってことかお?マイナスだったら右下がりだから右にずらして、プラスだったら左下がりだから左にずらす、ってことになるお。
![]() やらない夫
やらない夫
その通りだ。導関数は元の関数の傾きを表しているからな。微分して導関数を求めて、その符号によって $x$ の位置をずらす、別の言い方をすると $x$ を更新していくことで、最小値を求めるんだ。$x$ の更新を式にするとこうだな。
$$ x := x - \eta\frac{d}{dx}g(x) $$
![]() やらない夫
やらない夫
この手法を最急降下法と言う。
![]() やる夫
やる夫
$\eta$ って、なんだお?
![]() やらない夫
やらない夫
$\eta$ は、学習率と呼ばれる正の定数だ。学習率が小さければ、$g(x)$ の最小値にたどり着くまでに何度も $x$ を更新する必要があって、時間がかかってしまう。逆に学習率を大きくすれば、速く $g(x)$ の最小値にたどり着ける可能性があるが、$x$ が定まらず発散してしまう可能性もある。
![]() やる夫
やる夫
ちょっと待つお…、よくわからんお。
![]() やらない夫
やらない夫
そういう時はいつでも、簡単な値を代入して、具体的に確認してみるんだ。たとえば $\eta = 1$ として、$x = 3$ からスタートしてみるんだ。
![]() やる夫
やる夫
やってみるお。$g(x)$ の微分は $2x - 2$ だから、$x$ を更新する式は $x := x - \eta(2x - 2)$ になるお。右辺の $x$ にどんどん代入してみるお。
\begin{eqnarray}
x & := & 3 - 1(2\cdot 3 - 2) = 3 - 4 = -1 \
x & := & -1 - 1(2\cdot -1 - 2) = -1 + 4 = 3 \
x & := & 3 - 1(2\cdot 3 - 2) = 3 - 4 = -1 \
\end{eqnarray}
![]() やる夫
やる夫
これは大変だお!!無限ループするお!!!
![]() やらない夫
やらない夫
じゃぁ、今度は $\eta = 0.1$ として、同じく $x = 3$ からスタートしてみるんだ。
![]() やる夫
やる夫
やってみるお。面倒くさいから小数は、小数点以下 1 桁までで計算するお。
\begin{eqnarray}
x & := & 3 - 0.1\cdot(2\cdot 3 - 2) = 3 - 0.4 = 2.6 \
x & := & 2.6 - 0.1\cdot(2\cdot 2.6 - 2) = 2.6 - 0.3 = 2.3 \
x & := & 2.3 - 0.1\cdot(2\cdot 2.3 - 2) = 2.3 - 0.2 = 2.1 \
x & := & 2.1 - 0.1\cdot(2\cdot 2.1 - 2) = 2.1 - 0.2 = 1.9 \
\end{eqnarray}
![]() やる夫
やる夫
うーん、$x$ が 1 に近づいていってるけど、とても近づき方が遅いお…。小数点の計算、面倒だお…
![]() やらない夫
やらない夫
つまり、そういうことだな。$\eta$ が大きいと、$x$ をずらしすぎて、左に行ったり右に戻ったりを繰り返しているのがわかる。一方で、$\eta$ が小さいと、とても少しずつだが、$x$ が左にずれていっているのがわかる。
![]() やる夫
やる夫
なるほど。さすが、やらない夫だお。
![]() やらない夫
やらない夫
話を目的関数 $E(\theta)$ に戻すぞ。この関数は、変数として $\theta_0$ と $\theta_1$ の 2 つをもつ 2 変数関数だ。つまり各々の $\theta$ の更新を式にすると、こうだ。わかるか?
$$
\theta_0 := \theta_0 - \eta\frac{\partial E}{\partial \theta_0} \
\theta_1 := \theta_1 - \eta\frac{\partial E}{\partial \theta_1}
$$
![]() やる夫
やる夫
んー、ちょっと複雑になったけど、$g(x)$ が $E$ に変わって、偏微分になっただけだお。
![]() やらない夫
やらない夫
実際に $E$ を偏微分をしてみようか。まずは $\theta_0$ からだ。どうなる?
![]() やる夫
やる夫
えっ、あ、やる夫がやるのかお。えーっと…、あー、$\theta_0$ 自体は $E$ の中にはなくて、$f_{\theta}(x)$ の中にあるから、まずは代入しないといけなくて…、あ、2 乗されてるから、展開も必要だお。うっ、これは結構、面倒くさいお…
![]() やらない夫
やらない夫
正攻法だと少し面倒くさいから、合成関数の微分を使うともっと楽にできるな。
![]() やる夫
やる夫
ん、合成関数の微分?
![]() やらない夫
やらない夫
$f$ と $g$ という関数があったとき、これらの合成関数 $f(g(x))$ を $x$ で微分する場合はこうなる。これを使えば簡単になるぞ。
$$ \frac{df}{dx} = \frac{df}{dg}\cdot\frac{dg}{dx} $$
![]() やる夫
やる夫
お、これを目的関数に適用すればいいのかお?えっと…、こうかお?
$$ \frac{\partial E}{\partial \theta_0} = \frac{\partial E}{\partial f_{\theta}}\cdot\frac{\partial f_{\theta}}{\partial \theta_0} $$
![]() やる夫
やる夫
それぞれ計算してみるお。まずは $E$ を $f_{\theta}$ で微分するところから…
\begin{eqnarray}
\frac{\partial E}{\partial f_{\theta}} & = & \frac{\partial}{\partial f_{\theta}} \left(\frac{1}{2}\sum_{i=1}^n (y^{(i)} - f_{\theta} (x^{(i)}))^2\right) \
& = & \sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)})
\end{eqnarray}
![]() やる夫
やる夫
あー、ここで微分した時に次数の 2 が前に降りてきて、約分されて式が綺麗になるってわけかお。なるほど。次は $f_{\theta}$ の微分だお。
\begin{eqnarray}
\frac{\partial f_{\theta}}{\partial \theta_0} & = & \frac{\partial}{\partial \theta_0} \left(\theta_0 + \theta_1 x\right) \
& = & 1
\end{eqnarray}
![]() やる夫
やる夫
おっ、簡単になったお。この微分した結果 2 つを掛ければいいんだから…、答えはこうだお!あってるかお?
\begin{eqnarray}
\frac{\partial E}{\partial \theta_0} & = & \sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)}) \cdot 1 \
& = & \sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)})
\end{eqnarray}
![]() やらない夫
やらない夫
よし、いいぞ。$\theta_1$ に関しても、$E$ の微分はまったく同じだし、$f_{\theta}$ の微分は今度は $x$ になるな。要するに、$E$ を $\theta_1$ で偏微分した式はこうだ。
$$ \frac{\partial E}{\partial \theta_1} = \sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)})x^{(i)} $$
![]() やる夫
やる夫
合成関数の微分って便利だお。
![]() やらない夫
やらない夫
俺たちは、偏微分した結果を手に入れたので、結局は $\theta$ の更新式は以下のようになる。
\begin{eqnarray}
\theta_0 & := & \theta_0 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)}) \
\theta_1 & := & \theta_1 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)})x^{(i)}
\end{eqnarray}
![]() やる夫
やる夫
うーん、だいぶおぞましい式だお…
![]() やらない夫
やらない夫
実装するときの注意点だが、これら 2 つの $\theta$ は同時に更新していかなければならないんだ。$\theta_0$ を更新し終わった後に $\theta_1$ を更新しようとする時、更新済みの $\theta_0$ を使っていけない。更新前の $\theta_0$ を使うんだ。
![]() やる夫
やる夫
頭の片隅に置いとくお…
![]() やらない夫
やらない夫
これで、すべての道具はそろった。おさらいも兼ねて、まとめよう。
![]() やらない夫
やらない夫
俺たちは、攻撃力からダメージを計算するために、この未知の関数の切片と傾きを調べたかった。

![]() やらない夫
やらない夫
そのため、この関数を以下のように定義した。
$$ f_\theta(x) = \theta_0 + \theta_1 x $$
![]() やらない夫
やらない夫
そして、学習用データと、この関数の値の誤差を、以下のような関数で定義した。これを目的関数と呼ぶんだった。
$$ E(\theta) = \frac{1}{2}\sum_{i=1}^n (y^{(i)} - f_{\theta} (x^{(i)}))^2 $$
![]() やらない夫
やらない夫
俺たちのゴールは、この目的関数の値を最小化する $\theta_0$ と $\theta_1$ を見つけることだ。なぜなら、この目的関数は誤差の関数であり、誤差が小さければ小さいほど $f_\theta(x)$ の正しい形がわかるからだ。そのために、最急降下法を使って以下のようにパラメータ $\theta_0$ と $\theta_1$ を更新していく。
\begin{eqnarray}
\theta_0 & := & \theta_0 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)}) \
\theta_1 & := & \theta_1 - \eta\sum_{i=1}^n (f_{\theta} (x^{(i)}) - y^{(i)})x^{(i)}
\end{eqnarray}
![]() やらない夫
やらない夫
この更新のフェーズを学習と呼ぶことが多いな。更新を止めるタイミングは、目的関数の値が更新の前後であまり変わらなくなってきた時だ。もしくは一定回数だけ繰り返すという場合もある。
![]() やらない夫
やらない夫
具体的な $\theta$ の値がわかったら、あとはもう $f_\theta(x)$ に攻撃力を入れれば、ダメージが出力される。これでめでたく目標達成だ。
![]() やる夫
やる夫
単純な一次関数の形を見つけるだけなのに、たいした苦労だお…
![]() やらない夫
やらない夫
最初にも言ったが、これは問題設定が単純なので、あまり嬉しさが伝わらないかもしれないが、実際はもっと複雑な問題を解きたいことが多い。次はもう少し複雑な例を見てみるか。
![]() やる夫
やる夫
ちょっと疲れたから、休憩するお…