この記事は Math Advent Calendar 2015 の 14 日目の記事です。
他のブログが本格的な数学のお話を記事にしている中、僕はというとそんなに高度な数学の話ができるわけではないので、自身の数学との関わり方や、また今年に入って開催してきた プログラマのための数学勉強会@福岡 の振り返りとその今後についてを書いていきます。同じような境遇の人が少しでもこっち側の世界に足を踏み入れれるようになることを願って。
プログラマから見た数学の楽しさ
アルゴリズムやディープラーニング、ビッグデータ、WebGL など、よく聞くいわば流行りのワードについて、そういうものを使った技術やサービスを見つけた時「実際、中身はどういう風に動いているんだろう?」という好奇心はプログラマであれば潜在的には誰でも持っているのではないでしょうか。それは私達プログラマが、普通の人よりもより身近に普段からそういうことに接しているからだと思いますし、何よりも夢があるからです。
Google は画像を投げるだけで高速に画像の中身を識別できるようになりました。Facebook は顔写真から個人を予測することができるようになりました。映像や 3D の技術を使ったプロジェクションマッピングなども有名になりました。最先端の技術には夢が詰まっています。
ご存知のように、そういった技術の背後には高度な数学な知識が必要なものもあります。完全に理解するのはとても無理かもしれません。でも、それでも数学を知っているのと知っていないのでは、そういった技術をより身近に感じることができるかどうかには雲泥の差があります。
前にも書きましたが、数学という道具はプログラミングにおいて必ずしも必要なものではありません。しかし数学はプログラミングにおいて視野を広げるための武器になり得ます。ディープラーニングの仕組みがわかると楽しいし、ましてや自分で実装ができた日には興奮して眠れないことでしょう。
考えることの楽しさ
数学にはもう一つ僕が好きな側面があります。考える事の楽しさです。たとえば数学にはよく「公式」というものが出てきます。二次方程式の解の公式 (1) とか、三角関数の加法定理 (2) (3) とか。
$$ x = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \tag{1} $$ $$ \sin(\alpha+\beta) = \sin\alpha\cdot\cos\beta + \cos\alpha\cdot\sin\beta \tag{2} $$ $$ \cos(\alpha+\beta) = \cos\alpha\cdot\cos\beta - \sin\alpha\cdot\sin\beta \tag{3} $$
中学生や高校生の頃、こういう式はよく暗記していたと思います。でも歴史上初めてこれを発見した人達は、何かしらの方法でこれらの公式を導出してきたはずです。そして同様に僕達も丸暗記なんてしなくても、いろんな方法で公式を「導出」することだってできるのです。もちろん暗記が完全に悪というとそうではないと思います。我々には有限の時間しかありませんので効率よく知識を頭に詰め込んでいく必要があります。
ただ、それだけだと数学はまったくおもしろくありません。数式を見つめて、数式をいじって、数式と戯れます。裏に隠れてるものを見つける努力をします。代数的な解釈や、図形的な解釈もしてみます。グラフを書くのも良いです。そうやって自分で「考えて」みます。一見、まったく関係のないように見えることでも実は繋がっていたりします。
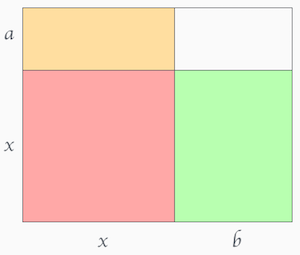
$(x+a)(x+b)=c$ という式をみて何を思い浮かべるでしょうか。とりあえず $x^2 + ax + bx + ab = c$ という風に展開するのは誰でも思いつきそうです。$x$ について解いてみますか?$x \ge 0, a \ge 0, b \ge 0$ という条件を付け加えて、縦が $(x+a)$ で、横が $(x+b)$ という長方形の面積が $c$ になる、という解釈をしてみるのもありでしょう。下図の赤は $x^2$ 、黄色は $ax$ 、緑は $bx$ 、白は $ab$ なので、全部たすと長方形の面積 $c$ になるし、実際にさっき展開した式と一致しています。
思えば、僕はそういうこと、つまり公式を暗記して問題を解くばかりが正解ではなく、自分で考えることの楽しさに気付いてから数学がとても好きになったのでした。たくさんの数式や問題を見て、そして考えて、背後にある繋がりを見つけたり、美しい式やグラフにうっとりしたり。題材は無限にあります。暗記せずに考えてみましょう。
数学ができないなりの楽しさ
とはいえ、そんなに「考える」と言われても、その土台となる経験や知識を持っていないとどうにもならないこともあります。実際に僕もしょっちゅう詰まります。そのためには長く根気強く数学と付き合っていく必要はあります。
話は変わりますが、私は今年の中旬から福岡でプログラマのための数学勉強会という勉強会を主催してきました。実はプログラマのための数学勉強会を開催する時も悩みました。自分は数学科卒でもないし、博士なんか持ってない、それに別に数学が極めて得意なわけでもないし、こんな自分が数学に関する勉強会なぞ主催していいんだろうかと不安に思っていました。
他の理由もあって、最初は開催は無理だろうと思っていましたが、Twitter のフォロワーや、東京の勉強会の主催者である @taketo1024 さんからの後押しもあって開催に踏み切ることができました。それからは、数学が得意じゃないからというような理由はもう考えないようにしました。無意味な恐怖心が邪魔をしていただけだと思います。
僕はただ数学が好きですし、そういう想いを通して数学好きな人と知り合いになれれば嬉しいなと思ったし、そういうことを伝えるために立場も何も関係ないんじゃないかな、と。何よりも、交流ってやっぱり楽しいんだし。
プログラマのための数学勉強会とは
結局は、プログラマのための数学勉強会を通して伝えたかった僕の想いとしては、やっぱり数学って楽しいよっていうことです。数学自体も楽しいし、その先に見えるものは、プログラマとしての自分をもっとワクワクさせてくれます。
まだ 2 回しか開催していませんが、幸いにも一定数の参加者には来ていただいていますし、来年になってもモチベーションを失わない限りは隔月くらいで続けていきたいという気持ちはあります。これからもっと一緒に楽しめる人が増えればとてもうれしいです。
数学資料まとめ
チラ裏だけで終わるのもアレなので僕が読んだことのある、無料の数学関連の文書を貼っておきます。主に大学レベルのものばかりですが、お金払って勉強を始めるには敷居が高いなぁと感じている方にはオススメです。
-
線形代数の基礎となる単語や概念が解説されている Web サイトです。
-
上記と同じく線形代数の基礎です。こっちは PDF なので、ダウンロードしてオフラインでも読めますが、ページ数がかなり多くて読むのがちょっと大変かも。
-
微分積分の基礎です。図が多くてわかりやすいです。
-
フーリエ変換に関する入門記事です。会話形式で話が進んでいき図の挿入もあり、とてもわかりやすいです。PDF もあります。
-
プログラミングのための確率統計という本の下書き PDF です。ページ数がかなりありますがとてもわかりやすいです。私はこの下書きを読んだ後に実際に本を買って読みましたが、下書きでも十分な内容だと思います。
-
少し純粋な数学からは離れるかもしれませんが、暗号技術の話です。