けんごのお屋敷

2015-01-10

バーテックスシェーダによる座標系変換

OpenGL 基礎シリーズの第 3 回です。

座標変換

プリミティブの描画には頂点座標が必要なのはわかった。だって、座標情報がないとそもそもどこに描画していいのかがわからないんだから。でもよく考えてみて欲しい、この座標情報って どの座標系における座標 なんだろう？それって最初に出てきた右手座標系とかいう座標系じゃないの？うーん、そうなんだけどここで話したいのはそういうことじゃない。それじゃディスプレイ上の座標に配置してるに決まってるよ！いやいやそんなことはない。私達は今、OpenGL 上で 3D 空間を扱っている。でも現実のディスプレイは 2D の平面。はい、これらはそもそも次元が違う。

最初にバーテックスシェーダの概要を書いた時に座標系の変換過程を図に示したのを思い出してみると、3D 空間を扱うためには少なくとも 4 つの座標系があった。最初に頂点座標を配置した座標系から最終的にはクリッピング座標系という座標系に変換していく必要があり、それこそがバーテックスシェーダの役割である。そして前回の記事で頂点座標を定義した時、その (x, y, z) で表される頂点座標は、実はローカル座標系における座標を指定していたのだ！ドヤァー

突然ドヤァーされても意味わからないと思うので詳細を見てみよう。

変換行列

では実際バーテックスシェーダで座標系の変換をするっていっても、それってどうやればいいのか。答えは行列です。行列というと高校数学程度の知識が必要になりそうだけど、行列の生成や演算など面倒なことは全て CPU や GPU がやってくれる。私達に必要なのは、どういう変換行列の種類があって、それをどのように組み合わせて利用するのか、ということだけなので「自分理系じゃなかったんだけど…」という人でも心配はない。便利な世の中〜。

とはいえ、実際にどういうものかぐらいは頭に置いておいたほうがイメージしやすいので、絵に書いてみると行列ってこういうもの。いろいろ難しそうな表現があるけど、わからないならわからないで深く理解しなくても大丈夫な領域ではあるので不安にならずに先に進んで大丈夫だと思う。もし知りたければ適当にググれば解説サイトはいっぱい出てくる。

行列演算

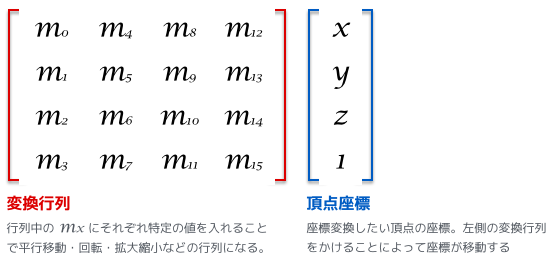
※頂点座標は (x, y, z) の 3 次元だったけど図の青枠で囲ってある頂点座標は 4 つになっている。最後の 1 ってなんだろう？これは頂点座標と変換行列の演算を単純にするために導入される 同次座標系 という新しい概念になるのだけど、この話を詳しくしだすと OpenGL から飛び出してしまうのでここでは割愛する。最後の 1 はよくある おまじない だ。。 。

では、前提知識をつけたところで実際にどういう風に座標系が変換されていくのかを見ていく。長い長い座標系変換への旅へ出発。

ワールド座標変換

まずはワールド座標変換。ジョジョじゃないよ。

Picture by Hay Kranen / CC-BY

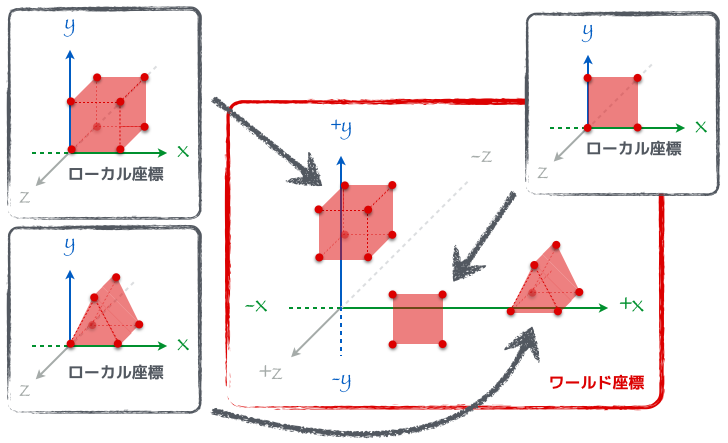
ポリゴンが組み合わさって何かしらの形を作っているものは「モデル」と呼ばれ、通常は大量のポリゴンを組み合わせて「人のモデル」とか「木のモデル」とか複雑なものが定義される。ここに表示しているのは ユタ・ティーポット と言って、これもモデルの 1 つで CG の分野では有名なモデル。こういったモデルはそのモデル専用のローカル座標を持っており、通常は頂点座標はこのローカル座標系の座標を表している。

そしてワールド座標変換とは、そういったローカル座標で定義されている各モデルを OpenGL 唯一の世界の座標に配置していく作業のことを言う。以下の図では立方体のモデル、三角柱のモデル、四角形のモデル、をそれぞれローカル座標系からワールド座標系へ変換している。こうしてみるとまるで OpenGL の世界の神様になったみたい。ワールド座標変換に使われる行列は

  • 平行移動
  • 拡大縮小
  • 回転
  • せん断

の 4 つがある。Android には android.opengl.Matrix クラスにそれぞれの行列を生成するためのメソッドがあるので、それらと共に紹介する。

ワールド座標変換

※ちなみにせん断については個人的には 2D ではあまり使いドコロがなく良く理解もしていないし android.opengl.Matrix クラスの中にせん断行列を生成してくれるメソッドが見当たらないので説明は割愛する。

平行移動

Android では Matrix.translateM メソッドの呼び出しで平行移動行列が生成される。前に呼んでいる Matrix.setIdentityM は単位行列を作るためのメソッドで、行列を生成するにはまず単位行列の形にしておいてそれを生成メソッドに渡すようにする。

float[] translationMatrix = new float[16];

Matrix.setIdentityM(translationMatrix, 0);
Matrix.translateM(translationMatrix, 0, x方向の移動量(tx), y方向の移動量(ty), z方向の移動量(tz));

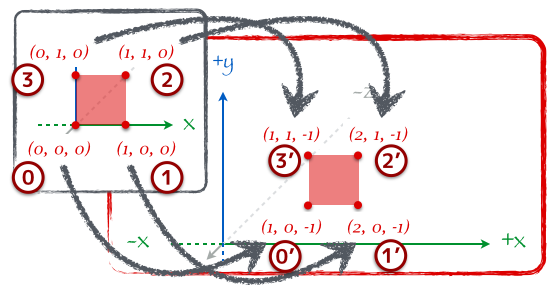
このメソッドによって生成される行列は以下の様なものになる。tx に 1 を指定すれば x 方向に +1 だけ座標が移動するし、ty に -1 を指定すれば y 方向に -1 だけ座標が移動する。この行列をモデルの各頂点にかけてあげれば平行移動した新しい座標のできあがり。

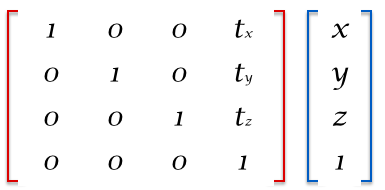
平行移動行列

拡大縮小

Android では Matrix.scaleM メソッドの呼び出しで拡大縮小行列が生成される。

float[] scaleMatrix = new float[16];

Matrix.setIdentityM(scaleMatrix, 0);
Matrix.translateM(scaleMatrix, 0, x方向の拡大縮小量(sx), y方向の拡大縮小量(sy), z方向の拡大縮小量(sz));

このメソッドによって生成される行列は以下の様なものになる。sx に 2 を指定すれば横方向の長さ(幅)が 2 倍に伸びるし、sy に 0.5 を指定すれば縦方向の長さ(高さ)が半分になる。

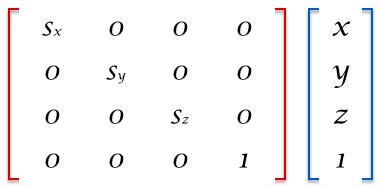
拡大縮小行列

回転

Android では Matrix.rotateM メソッドの呼び出しで回転行列が生成される。

float[] rotateMatrix = new float[16];

Matrix.setIdentityM(rotateMatrix, 0);
Matrix.translateM(rotateMatrix, 0, 回転角度θ, x軸(rx), y軸(ry), z軸(rz));

θ を指定して rx を 1 とすれば x 軸を中心として、ry を 1 とすれば y 軸を中心として回転することになる。ちなみに回転行列は中心とする軸によって行列が異なるので、以下のように x、y、z それぞれの軸を中心として回転する 3 種類の回転行列がある。

回転行列

このような平行移動、拡大縮小、回転の行列をモデルの全ての頂点に対して掛けていくことで、ワールド座標系にモデルを配置していくことになる。四角形のモデルであれば頂点数は 4 つなので 4 回の行列演算が行われる。立方体であれば頂点数は 8 つなので 8 回の行列演算。そしてもっと複雑な、たとえば人間のモデルともなると頂点数は数万にのぼることもあるので、その場合は数万回の行列演算が行われることになる。ひえ〜。

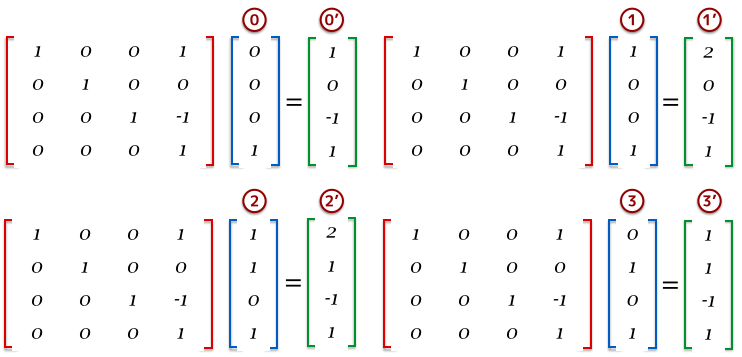
少しでもワールド座標系への変換のイメージをつけることができたらいいけど、例えば四角形モデルの各頂点を平行移動する様子はこんな感じになる。この例では四角形モデルを x 座標に +1、z 座標に -1 だけ平行移動している。

平行移動の例

ビュー座標変換

世界の神様になってモデルを各箇所に配置していく感覚には慣れただろうか。次はビュー座標変換というものを扱う。ここからはカメラの話が出てきてなんとも 3D っぽくなってくる。そもそもカメラとはなんだろう？カメラは同じものが現実世界にもあってすごくわかりやすい。スマホのカメラや一眼レフでも使い捨てカメラ (懐かしいな) でも何でもいいけど、シャッターを押すことで 現実世界の一部を切り取って 写真にしてくれるよね。そして、シャッターを押す時は「はいチーズ！コナンくん！」『バーローｗｗｗ』とか言いながら カメラを被写体に向けて シャッターを押すのである。

OpenGL のカメラもこれと同じで、ワールド座標に配置したモデル達にカメラを向けることで、そのカメラがディスプレイに表示する世界を切り取ってくれる。さて、カメラのパラメータとして必要な情報は以下の 3 つがある。

  • カメラの位置
  • カメラが見ている位置(注視点)
  • カメラの上方向

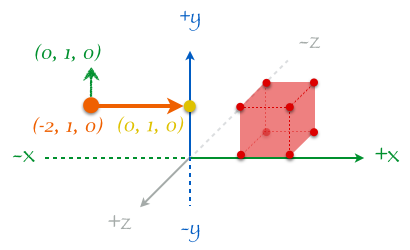
この 3 つのパラメータが決まればカメラが切り取る世界の景色が見えてくる。カメラはどこに置いても構わないし、どこを見ていても構わないので、たとえばワールド空間にこんな風にカメラを配置できる。この場合、カメラの位置が (-2, 1, 0)、カメラが見ている位置が (0, 1, 0)、カメラの上方向が (0, 1, 0) となる。カメラの上方向は文字通り「方向」なので座標ではなく方向を表す単位ベクトルで指定することになる。

ワールド座標系へのカメラの配置

※カメラの上方向は正確にはカメラに対して前後に傾いていても問題はない、というか前後に傾いているだけであれば結果として見える景色は同じになって、左右に傾いているのであれば見える景色が違ってくる。上方向が前後に傾いていても景色が同じってのは直感には反するけど、よく考えてみたらカメラの位置と注視点という 2 つのパラメータが決まることでカメラのレンズの向きは決まる。カメラが前後に傾くってことはカメラのレンズの向きが変わる、つまり注視点が変わってる、ってことだ。なのでカメラの上方向で重要なのは前後の傾きよりは左右の傾きであって、その左右の傾きの量で切り取られた後の世界の回転量が決定される。

さてさて私達は今、原点が中心にある右手座標系のワールド座標空間を z 軸手前の方から見ており、そこの左上辺りにカメラを配置した。これは私達をメインとして、つまり私達が世界の中心となって世界を見ている。ビュー座標変換は、そんな人間原理的な我々中心で見ている世界から、カメラ中心で見る世界に座標変換することを言う。より具体的に言うと

  • カメラの位置を原点にもってきて
  • カメラが見ている位置を z 軸奥 (-z の方向) を向けて
  • カメラの上方向を y 軸上 (+y の方向) を向ける

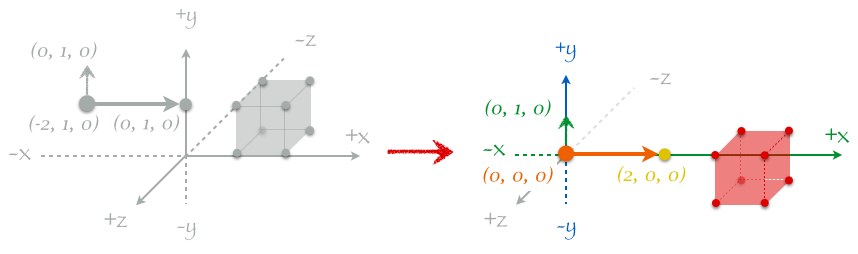
という変換を行う。先に示したカメラ配置でのビュー変換を直感的に見てみよう。まず、カメラの景色が変わらないようにカメラを原点に移動させてみる。つまりカメラを原点に移動させたらモデルもそれと同じ量だけ移動させる。カメラもモデルも右下の方にずれて、カメラが原点に配置されていることがわかる。これって、移動前と移動後でカメラの景色がかわらないのは理解できるかな？この変換はワールド座標変換で出てきた平行移動行列をモデルの各頂点に掛けるだけで簡単に変換できる。

カメラを原点に移動

次にカメラの向きを回転してみる。y 軸を中心として 90 度だけ左方向にグルっと回転して、カメラが z 軸奥の方を向くようにする。同じく景色が変わらないようにモデルの座標も回転させている。この変換も同様に、ワールド座標変換で出てきた回転行列をモデルの各頂点に掛けるだけで簡単に変換できる。ここでカメラの上方向が y 軸上を向いていない場合はさらに変換がかかるが、これもカメラの向きを変えた時同様にカメラの上方向が y 軸上を向くように回転行列を掛けるだけで変換できる。

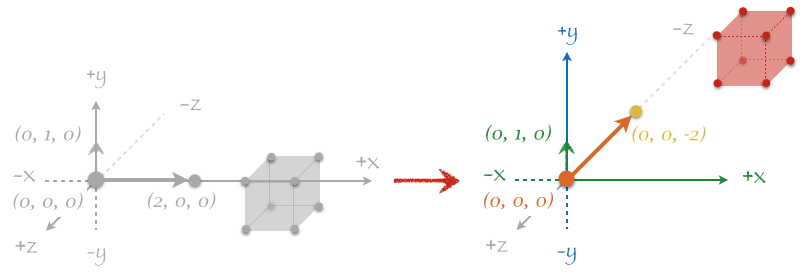
カメラの向きを回転

※直感的に理解できるように、カメラ用の新軸の定義について説明を端折っているし、座標変換の順番ややり方など実際と異なる部分もあるので、あくまで理解用の説明ということで。

これでビュー座標系への変換が完了した。この変換のための行列は Matrix.setLookAtM メソッドを使って作ることができる。

float[] viewMatrix = new float[16];

Matrix.setLookAtM(
    viewMatrix, 0,
   -2f, 1f, 0f, // カメラの位置
    0f, 1f, 0f, // カメラが見ている位置(注視点)
    0f, 1f, 0f  // カメラの上方向
);

射影変換

私達はモデルを OpenGL の世界に配置して、それからそこにカメラを置いて、さらにカメラ中心の世界に変換した。そして次はいよいよ最後、3D の世界を xy 平面上の 2D の世界に投影するための射影変換だ。3D から 2D の変換ってそんなに簡単にできるの？と直感的には思うけど、実はこれまでのワールド座標変換やビュー座標変換と同様に行列を使って一発で変換できる。行列ってすごいでしょ？

投影方法

一般的に投影方法には 透視投影 と 平行投影 の 2 種類がある。

透視投影

カメラの近くのものは大きく見えて、遠くのものは小さく見える、要は遠近感を扱うことができる投影方法。これは私達の感覚そのまま、現実の世界そのままの変換を行う。3D を扱うゲームやコンテンツはこの投影方法を用いている。

透視投影

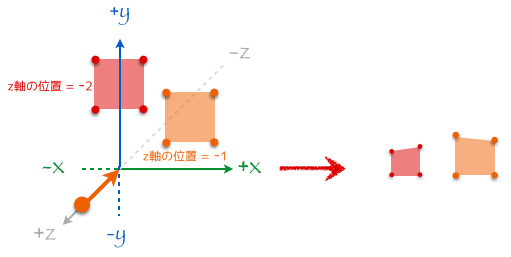
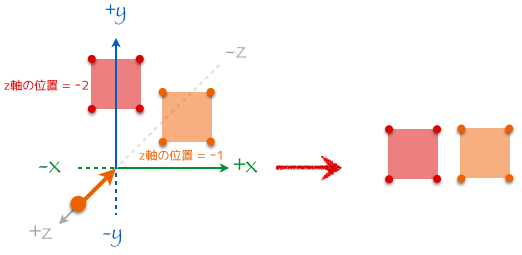
平行投影

カメラからの距離に関わらずモデルそのものの大きさがそのまま見える。現実世界の私達の感覚とはかけはなれているけど 2D を描画する時はこっちの方が便利。透視投影は平行投影より複雑だし、この記事では 2D を扱うことが目的なので射影変換にはこちらの平行投影を使っていく。

平行投影

クリッピング

射影変換のための行列を作るためにはどこからどこまでの領域を投影するのか、という視野空間の情報が必要になる。この視野空間内に存在するモデル達が実際に画面に表示されることになる。平行投影の場合、これに必要なパラメータは以下の 6 つ。

  • 左側の x 座標
  • 右側の x 座標
  • 下側の y 座標
  • 上側の y 座標
  • カメラから見た手前の z 座標
  • カメラから見た奥の z 座標

これらのパラメータをこちらから与えてあげることで以下のような視野空間が定義される。この時、カメラから見た時の z 座標は奥のほうをプラスとみなして指定する。

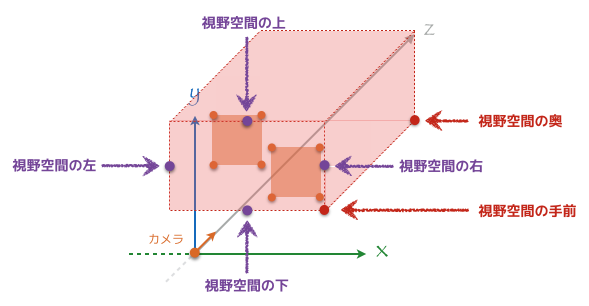
視野空間の定義

そしてこの視野空間を x軸、y軸、z軸、それぞれにおいて -1 から 1 の範囲におさまるように座標を変換してあげないといけない。これを 正規化 といって OpenGL が扱いやすいように変形をしてあげることを言う。

それでは実際に変換はどのようにやるのかというと、平行投影に限ってはこれまでのワールド座標変換やビュー座標変換のようにモデルを動かしたりはせずに、ビュー座標系に置かれた視野空間の中のモデルの頂点座標そのままを使うことが出来る。透視投影と違ってカメラからの距離によっての遠近感の演出がないためモデルの形が変わったりすることがないからね。えっ、じゃぁ平行投影の場合の射影変換って何するの？というと実は何もせずに、先に書いた正規化だけを行う。最終的に正規化されて出来た空間をクリッピング空間と呼び、その座標系のことをクリッピング座標系と呼ぶ。

※クリッピング座標系は正規化デバイス座標系と呼ばれたりもする。まあ呼び方なんてそんな躍起になって覚えなくてもいいんじゃないだろうか。ほんとうに大事なのは物事の本質、その座標系がどういうものなのか、っていうところだしね。

正規化は以下のような要領でやっていく。

  • 視野空間の中心が原点となるように視野空間内のモデルに平行移動行列を掛ける
  • 視野空間の幅、高さ、奥行きの長さが 2 になるように視野空間内のモデルに拡大縮小行列を掛ける

これだけ。どれくらい移動させれば原点まで動くのかとか、どれくらい縮小すれば視野空間が 2 x 2 x 2 になるのかとか、求めようと思えば簡単に計算できるけど、そういうのは全部 CPU がやってくれるのであまり気にしなくても良い。Android では平行投影用の行列を Matrix.orthoM メソッドで生成することができる。

float[] projectionMatrix = new float[16];

Matrix.orthoM(
    projectionMatrix, 0,
    視野空間の左側のx座標,
    視野空間の右側のx座標,
    視野空間の下側のy座標,
    視野空間の上側のy座標,
    カメラから見た視野空間の手前のz座標,
    カメラから見た視野空間の奥のz座標
);

※透視投影用の行列の生成は平行投影よりもっと複雑で、2D 描画にはあまり使われないのでこの記事での解説は割愛する。ただ、透視投影にも専用の行列を作るための perspectiveM というメソッドがあるので、行列の生成はそいつに任せれば良い。行列の生成方法に興味があるならネット上には多くの記事があるので気になる場合はのぞいてみるのも面白い。ここまで読み進められたモチベーションとここまでで蓄えられた知識があれば意外とスラスラ理解できるかもしれない。

まとめ

長い長い座標変換の旅がようやくこれで終わった。最初に頂点座標を配置するモデル座標から様々な変換行列を掛けあわせながら最終的にはクリッピング座標系まで変換される。変換過程をひとまとめにして一気に理解しようとするのは到底無理なことではあるが、このように 1 つ 1 つ分解して細かくして見てみるとなんとか理解できそうな気もする。

ここで作った座標変換行列は実際には OpenGL の API を使って頂点情報と同じように GPU に転送され、バーテックスシェーダの中で利用される。バーテックスシェーダでどういう実装をすればいいかの話はまた別にするとして、今回はバーテックスシェーダがどういう仕事をしているのかを主に説明してきた。いきなり実装の話をして意味不明なコードに怒りを募らせノートパソコンを窓から放り投げたくなるよりかは、先にこういった下地を理解しておくことで実装時には驚くほど「なるほど感」が出てくる。

次回 ラスタライザの画素生成と線形補間 に続く。

  • このエントリーをはてなブックマークに追加