OpenGL 基礎シリーズ の第 4 回です。

ビューポート変換

ラスタライザの話をするまえにもひとつ変換についての話を。バーテックスシェーダによって長い長い座標系変換の旅 (いやテキストだと長いけど GPU での演算は一瞬で終わるからね。一瞬で) をしてきた頂点達にとって最後の変換過程が残っている。それがビューポート変換というやつだ。

「とうとう現れたか、ビューポート変換め！」
『 グヘヘヘよく来たな頂点ども。 』
「臆することはない、ヤツは 座標系変換四天王の中でも最弱 。」

ということで簡単です。

バーテックスシェーダで最終的に変換されたクリッピング座標系は xyz 座標がそれぞれ -1 〜 1 の範囲に正規化された座標系だったけど、それを実際にオブジェクトを描画するディスプレイのサイズの座標に変換する。その際、次のラスタライズの処理に繋げるために xy 成分だけ取り出して平面にしておく。これをウィンドウ座標系といって、左下が原点 (0, 0) になる。たとえば描画先のディスプレイのサイズが 800 x 600 だった場合はこんな感じ。

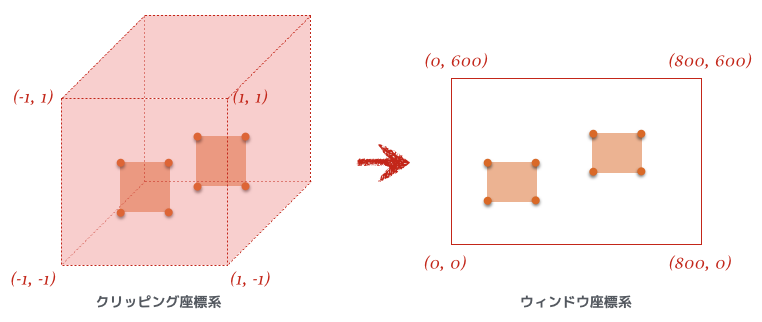
Android では以下のメソッドを呼び出すことでビューポート変換での幅や高さの設定ができる。

GLES20.glViewport(ディスプレイ左下のx座標, ディスプレイ左下のy座標, ディスプレイの幅, ディスプレイの高さ);

ところで残った z 座標はどこへ行くかというと、ポリゴンが重なっていた場合にその前後の位置関係を把握して重なりを制御するためにデプステストという工程がフラグメントシェーダの後にあるんだけど、そこで使われるために別途バッファに保存される。デプステストについては最初の目次に書いてないのでこのブログに出てくる予定はないけど、時間があればその仕組みを解説する記事をかいてみようかな。

ラスタライズ

それでは本題のラスタライズの話。バーテックスシェーダとビューポート変換によって最終的な平面上での頂点の位置が計算されたことで最終的なポリゴンの形もここで確定された。次はこのポリゴン達がディスプレイ上の (正確にはフレームバッファー上の) どのピクセルに描画されるのかを求める必要がある。前にも書いたけど、ラスタライズは描画するピクセルつまり画素を生成することを言い、生成された画素のことをフラグメントと言う。ここではどのようにラスタライズが行われ、そしてそれらのピクセルがどのようにフラグメントシェーダに渡されるのかを詳しく見てみる。この辺の話は 2D を扱いたい場合でも 3D を扱いたい場合でも変わりはない。

ラスタライズには以下の 3 つのプロセスがある。

• ポリゴンの裏表面の判別
• 表面のポリゴンが覆っているピクセルのフラグメント生成
• バーテックスシェーダから渡された値の線形補間

ポリゴンの裏表面の判別は頂点情報の話をした時にも書いたとおり、頂点インデックスを指定する順番によって変わる。裏表の判別が終わったら、次はフラグメントの生成に移る。ここでもしカリングが有効になっていれば裏面を向いたポリゴンは無視され、表面を向いているポリゴンが覆っているフレームバッファー上のフラグメントだけが生成される。カリングが無効になっていれば裏面ポリゴンも同様に処理される。そして最後にバーテックスシェーダから渡ってきた値 (たとえば頂点座標や法線情報、色情報、など) を生成されたフラグメント毎に線形補間して、フラグメントと一緒にフラグメントシェーダに渡してあげるといった流れになる。

フラグメント生成方法

OpenGL においてフレームバッファのある特定のピクセルのフラグメントが生成されるかどうかは、そのピクセルの中心がポリゴンの内側に位置しているかどうかによって決まる。以下の図は、各矩形が画面上の 1 ピクセルを表しており、その中にある赤い点がそのピクセルの中心点、そして赤い枠線がポリゴンの形になっている。中心点である赤い点が赤枠の内側にあるピクセルについては紫色で塗りつぶされており、これがラスタライズ処理によって生成されるフラグメントになる。そしてそれら 1 つ 1 つがすべてフラグメントシェーダに渡される。

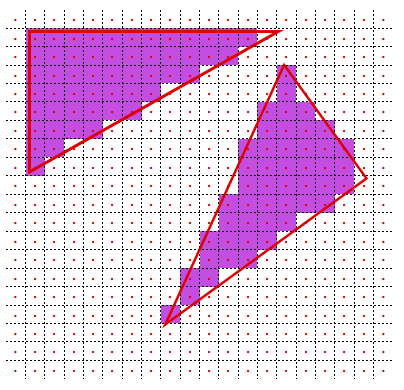
※本当はこれだけではなくて、複数ポリゴンが重なっていた場合や同じ辺を共有していたりする場合にはもう少し考えるべき事柄が増えることになるけど、その辺の実装は GPU によって違うらしいので、ここではあまり詳しく触れないことにする。

線形補間

今までバーテックスシェーダに頂点情報を渡して座標系を変換するという話をさんざんしてきたけど、実はバーテックスシェーダには頂点情報以外にも情報を渡すことができる。バーテックスって日本語では頂点って意味なんだけど、でも頂点以外の情報もどんとこい、と受け付けてくれる心優しいバーテックスシェーダ。というのは置いといて、頂点以外の情報って何さ？というと、たとえば頂点の色情報だったり法線情報だったり貼り付けるテクスチャの uv 座標情報だったり、本当に何でも送れる。頂点情報の付加情報としてね。法線とか uv とかまだこのブログ内では出てきてないのでわからないと思うけど、とりあえず無視して大丈夫。

そして今回はここがキモなのだけど、バーテックスシェーダに送られてきた情報はそのままフラグメントシェーダに渡すことができるようになっている。以下その詳細をつらつらと。

シェーダ毎の処理単位の違い

ここでは例えば頂点情報と色情報を一緒にバーテックスシェーダへ送ったとする。赤い文字が頂点座標を表していて、それ以外の色が付いた文字が頂点の色情報を表している。

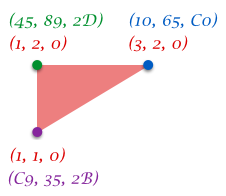
ここでバーテックスシェーダからフラグメントシェーダに色情報を送ることを考えてみる。でもちょっと待ってほしい。思い出して欲しいのだけど、バーテックスシェーダとフラグメントシェーダは処理単位が違う。ん、どういうこと？つまり

• バーテックスシェーダは頂点毎に呼び出される
• フラグメントシェーダはフラグメント毎に呼び出される

ということ。ラスタライズまでの流れは簡単には以下ようなフローになっていて、見て分かる通りバーテックスシェーダとフラグメントシェーダは処理単位が違う。この時、フラグメントシェーダに色情報を渡すことを考えると、左上と右上と左下のフラグメントはそのまま頂点の色を渡せばよさそうだけど、じゃぁ真ん中辺りのフラグメントはどの頂点の色情報を渡せばいいの？ということになる。今回は左上の色を渡して、次回は右上の色を渡して、なんていう気まぐれなシェーダではとても困る。

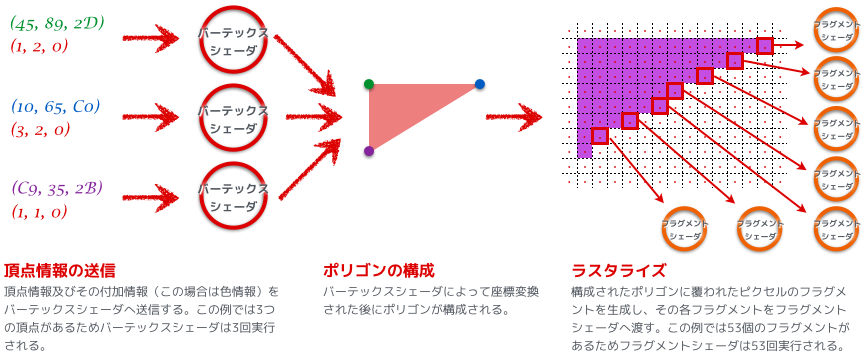
ラスタライザはこの問題を、バーテックスシェーダからフラグメントシェーダに渡されるべき情報を自動的に補間することで解決するのだッッ！！

重心座標系

だッッ！！と言われても、えっ？という人がほとんどだと思うのでもう少し詳しく見てみると、補完するとはつまりポリゴンのある特定の位置のフラグメントについて 「最初の頂点の色は 50% だけ使って、次の頂点の色 20% だけ使おう、そして最後の頂点の色は 30% だけ使って、これらを全部足しあわせたものをフラグメントシェーダに渡そう」 という風に決めることを言う。ほうほうなるほど、そしたらその 何パーセント持ってきて という情報はどうやって決めてるんだろう。

ちょっと下の三角形を見てみよう。3 つの頂点 (A, B, C) と、その三角形の中に位置する点 P がある。するとその点 P を中心として三角形の中にさらに 3 つの三角形 T1 T2 T3 が作れるのがわかる。えーっと、こんな風に記号がいっぱい出てくるとなんだか突然数学っぽくなってくるけど、難しい数式とかは出てこないので安心してじっくり読み進めて大丈夫。

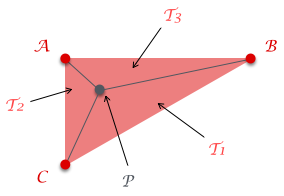
さて話を進めるけど、今回この点 P の位置にあるフラグメントについて、フラグメントシェーダに渡る色情報は何になるのか？というのを求めようとする場合、今この図に書いてある情報を使って計算することができる。まず 3 つの頂点 (A, B, C) で構成される三角形の面積と、T1 T2 T3 の三角形の面積を求める。するとその求めた面積を使って T1 T2 T3 のそれぞれの比率を求めることができる。このようにして求めた T1 T2 T3 のそれぞれの面積の比率が、最初に書いた 何パーセント持ってきて という情報に当たる。ちと文章で書きなぐっただけではわかりにくいので、具体的な値を入れて計算してみると

• (A, B, C) の面積を 100 とする
• T1 の面積を 50 とする
• T2 の面積を 20 とする
• T3 の面積を 30 とする
• T1 の比率は 50 / 100 = 0.5
• T2 の比率は 20 / 100 = 0.2
• T3 の比率は 30 / 100 = 0.3

という風になってこれは頂点 A の色を 50%、頂点 B の色を 20%、頂点 C の色を 30%、それぞれ使ってそれらを足し合わせることになる。これは色情報だけではない。例えがわかりやすいので色情報の話をしていただけで、他のどんな情報も、つまりバーテックスシェーダからフラグメントシェーダに渡される全ての情報は、このような手順で値が補完される。

※ここの説明に使った図ような、図形の中にある特定の点をとってその点がその図形の中でだいたいどの辺りにいるのかな〜というのを調べる時に便利なのが重心座標系というもので、なんか名前がカッコいいので覚えておくとどこかでﾄﾞﾔｰできるかも。

まとめ

ラスタライズについては OpenGL でプログラミングをしていく上でプログラマが知らなくても開発に支障をきたすことはない。実際は私も OpenGL に触れ初めの頃は、ラスタライズという処理があることすら知らずにしばらく開発をしていた。でも中身をより詳しく理解することによって OpenGL だけじゃなくて 3D や CG の世界にまで広がって基礎を押さえることができる。そして何より「わかる」ということはとても面白い。

頂点情報や座標変換の話に比べてボリュームは小さかったけど、まあ OpenGL で何かを描画するまでにはこういう処理があるんだよ、という程度の認識で先に進んでも大きな問題はない。

次回 テクスチャマッピング に続く。