OpenGL 基礎シリーズの第 2 回です。
OpenGL の座標系
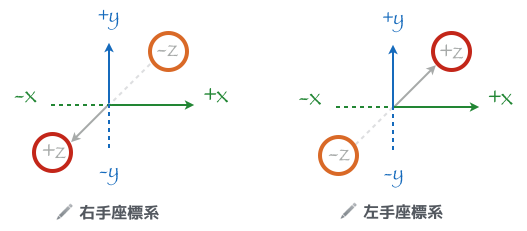
まず頂点の話をする前に前提として知っておかなければならない座標系の話がある。私達が 3D の世界を扱う時は 右手座標系 と 左手座標系 という 2 つの座標系が存在する。それぞれの違いは z 軸の向き。
- 右手座標系は z 軸の手前の方がプラス、z 軸の奥のほうがマイナス
- 左手座標系は z 軸の手前の方がマイナス、z 軸の奥のほうがプラス
3D の座標を扱う時はこの座標系のどちらかを採用しており、我らが OpenGL ではポリゴンを配置する時の座標系は右手座標系を使う。この右手座標系は数学の世界で使われている座標系で OpenGL がこれを採用したのはそれが理由と言われている。(※ちなみにご存知 Windows の DirectX 3D は標準では左手座標系を採用している)
2D を扱うにあたって遠近感を出すために z 軸を意識することはあんまりないけど、描画する要素の重なりを制御するために使うことはよくある。ゲームなどで画像を重ねて描画するにあたっては z 軸の奥の方がプラスになってる方がわかりやすく、右手座標系のように z 軸の手前の方がプラスになっているのは違和感がある人が多いかもしれないけど、自分の感覚と違ってもそこだけは間違えないようにしないと、背景の方がキャラクターより前にきてしまって、あれ?なんでキャラクターいないの?という風に思った通りの描画が出来なくなってしまうので要注意。
※ちなみになんで右手と左手というんだろうか?それは、親指の先を x 軸プラス方向、人差し指の先を y 軸プラス方向、中指の先を z 軸プラス方向と思って、実際の座標系の軸を手を使って形作ってみるとわかる。右手でそれをすると中指が自分の方向を向いて、左手でそれをすると中指が向こう側を向くはずだ。こういう単純でどうでもいいことでも、理由がわかって納得できると面白いですよね?
プリミティブ
もう何度も言ってる気がするけど OpenGL では 3D の頂点情報 (x, y, z) を定義して、それを GPU に転送することで描画を行う。それによって描画されるものを プリミティブ と言って、OpenGL の世界で描画できる最小単位のことを言う。また新しい言葉が出てきた!ってひるまないひるまない。ただ単に言葉の定義だけ。で、プリミティブには以下の 3 種類がある。
- 点 - 頂点数 1
- 線 - 頂点数 2
- ポリゴン(三角形) - 頂点数 3
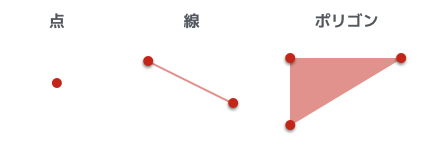
OpenGL ではポリゴンに色をつけて描画することが、そのまま図形 (三角形や四角形) を描画することになる。
ポリゴンは「多角形」という意味だけど OpenGL では実は三角形のポリゴンしか描画できない。えっ、なにそれ?使えないじゃん?!という疑問を持つのは当然だけど、三角形は 他の多角形と比べて単純 という性質を持っているので、その性質を利用することで GPU の計算量を減らすことができる。とはいえ三角形以外の多角形も描画できないとやってられなーい、ってことになるけどでもね、実は全ての多角形は三角形の組み合わせで表現することができるようになっているし、少し工夫すれば円にも近似することができるのでまったく問題はない。
頂点情報の準備
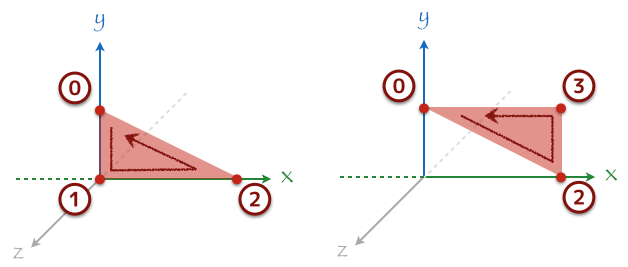
という話をしたところで、それでは早速以下の図のような四角形のポリゴンを描画することを考えてみる。これを描画するにはどのような情報が必要になるのだろう?
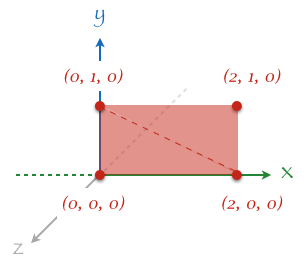
頂点座標
図を見て分かる通り四角形を描画するためには 4 つの頂点が必要になる。ただし、先にも説明した通り OpenGL では三角形のポリゴンしか描画できないので、以下の三角形を 2 つ組み合わせて四角形を表現する。
- 1 つ目の三角形(左下の方)
(0, 1, 0)-(0, 0, 0)-(2, 0, 0) - 2 つ目の三角形(右上の方)
(2, 0, 0)-(2, 1, 0)-(0, 1, 0)
ね、三角形の組み合わせで四角形を表現できたでしょ?他の多角形の場合も同様に三角形の数が多くなるだけで、ちゃんと三角形だけで表現できる。さて話がそれた。三角形 2 つとしてみると頂点座標は 6 個あるけど、そのうち 2 つは重複してるので実際に定義するのは 4 つで良い。
float[] vertices = new float[] {
0f, 1f, 0f, // 左上 (0番目の頂点)
0f, 0f, 0f, // 左下 (1番目の頂点)
2f, 0f, 0f, // 右下 (2番目の頂点)
2f, 1f, 0f // 右上 (3番目の頂点)
};
頂点インデックス
頂点座標が決まったら次はどの頂点で三角形を描画するのかを GPU に教えてあげる必要がある。座標を指定した順番で描画してくれればいいじゃないか!って思うけど、まあ実はそういう風に描画することもできる。でも頂点インデックスという考え方を身につけておいたほうが後々楽になってくるので、とりあえず読んでみよう。まずわかりやすいように図中に頂点の番号を書いてみる。この番号は上の方に書いてるサンプルコードで頂点座標を new float[] { ... } した時に定義した順番と同じで、コメントに「x 番目の頂点」と書いてあるその x と一致する。
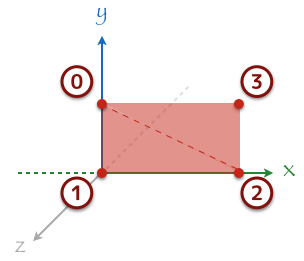
この頂点の番号 (この番号のことを頂点インデックスと言う) を使ってどういう三角形を描画するのかを親切に GPU に教えてあげる。以下のような配列を定義してそれを GPU に転送することで、指定された 3 つの頂点をつなげて以下のような三角形のポリゴンを得ることができる。
short[] indices = new short[] {
0, 1, 2, // 1つ目の三角形を構成する3つの頂点の番号
2, 3, 0 // 2つ目の三角形を構成する3つの頂点の番号
};
カリング
わざわざ頂点インデックスをたどる順番に矢印をつけたのは意味があって、実はポリゴンというのは裏表を持っている。な、なんだってー!ポリゴンの裏表をどうやって判断するかというと
- 反時計回りに頂点インデックスを指定していくと表になる
- 時計回りに頂点インデックスを指定していくと裏になる
という風に指定した頂点インデックスの順番を見て裏表を判断している。そして OpenGL ではカリングといって、高速化のために裏面のポリゴンを描画しない機能がある。
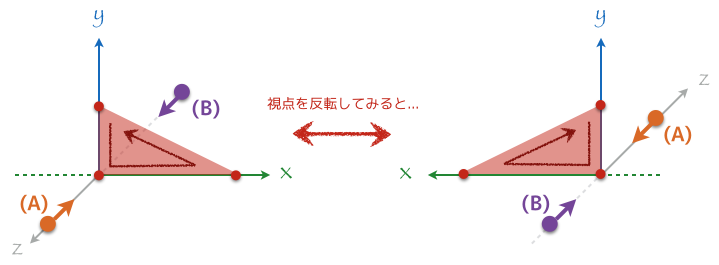
ポリゴンの裏表については下の図のように A さんと B さんをそれぞれ z 軸上に y 軸を挟んで反対側に置いてみるとわかりやすい。A さんから見た三角形は反時計回りで頂点インデックスが指定されているから表向きになるんだけど、B さんから見た三角形は時計回りに指定されているので裏向きになる。今後の話に出てくることになるけど、この A さんと B さんはカメラに置き換えることができる。カメラがどこから世界を見ているかによって、ポリゴンの表面が見えたり裏面が見えたりすることになり、裏面が見えていれば描画させないようにすることができる。
とはいえ 2D の場合だと z 軸の奥の方を見るようにカメラが固定されることが多いし、立方体のようなポリゴンは作らずに平面ポリゴンだけ使えば事足りると思うので、あまりカリングについて意識することはない。ただ頂点インデックスの順番によってはカリングの機能が ON になっていると描画されないこともあるよ、という程度の認識を頭の片隅にでも置いておけば大丈夫。
描画モードの指定
頂点座標と頂点インデックスが用意できたら、あと決める必要があるのは描画モード。描画モードとは頂点座標と頂点インデックスを使ってどんな風にプリミティブを描画するかどうかを決めるものだ。まだ何か決めることがあるの?もう…と思った人、これで最後です。
描画モードは以下の 7 種類がある。(本家 OpenGL はもう少し種類がある)
- GL_POINTS
- GL_LINES
- GL_LINE_STRIP
- GL_LINE_LOOP
- GL_TRIANGLES
- GL_TRIANGLE_STRIP
- GL_TRIANGLE_FAN
POINT が点、LINE が線、TRINGLE が三角形、を作るための描画モードということは何となくわかる。それぞれ詳しく見てみよう。以下の様な頂点座標と頂点インデックスが指定されている前提で話を進めていく。

コードで書くとつまりこういうことだ。
float[] vertices = new float[] {
x1, y1, z1, // 左下 (0番目の頂点)
x2, y2, z2, // 右下 (1番目の頂点)
x3, y3, z3, // 左真中 (2番目の頂点)
x4, y4, z4, // 右真中 (3番目の頂点)
x5, y5, z5, // 左上 (4番目の頂点)
x6, y6, z6 // 右上 (5番目の頂点)
};
short[] indices = new short[] {
0, 1, 2, 3, 4, 5
};
GL_POINTS
描画モードに GL_POINTS を指定すると頂点座標がそのまま点として描画される。超単純。
GL_LINES / GL_LINE_STRIP / GL_LINE_LOOP
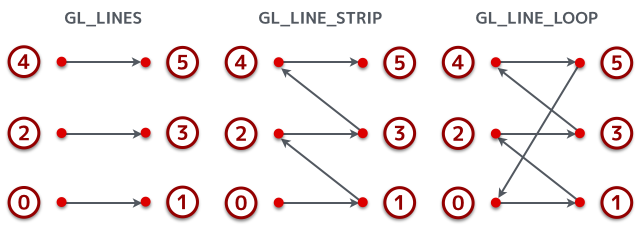
これらの描画モードでは線が描画される。各モードのおおまかな違いは指定された頂点を再利用するかどうか、という点だ。以下まとめてみた。
| モード | 描画方法 | 線の座標 | 線の数 |
|---|---|---|---|
| GL_LINES | 頂点を再利用しない | (0, 1) (2, 3) (4, 5) |
3 個 |
| GL_LINE_STRIP | 前回の線に使った頂点を 1 つ再利用する | (0, 1) (1, 2) (2, 3) (3, 4) (4, 5) |
6 個 |
| GL_LINE_LOOP | 前回の線に使った頂点を 1 つ再利用して 最初と最後の頂点も利用される |
(0, 1) (1, 2) (2, 3) (3, 4) (4, 5) (5, 0) |
7 個 |
GL_TRIANGLES / GL_TRIANGLE_STRIP / GL_TRIANGLE_FAN
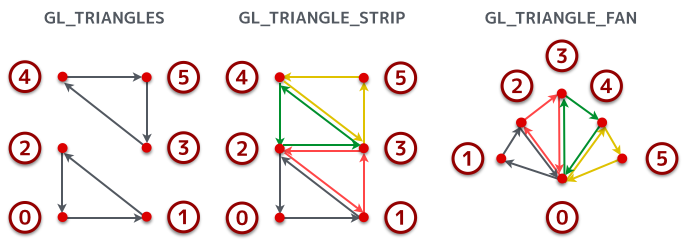
これらの描画モードでは三角形が描画される。線の時と同じように各モードのおおまかな違いは頂点を再利用するかどうか、という点だ。GL_TRIANGLE_FAN については頂点の再利用のされ方がちょっと違うので、それだけは見た目にわかりやすいように他とは違う頂点座標で例を示している。
| モード | 描画方法 | 三角形の座標 | 三角形の数 |
|---|---|---|---|
| GL_TRIANGLES | 頂点を再利用しない | (0, 1, 2) (3, 4, 5) |
2 個 |
| GL_TRIANGLE_STRIP | 前回の三角形に使った頂点を 2 つ再利用する | (0, 1, 2) (1, 3, 2) (2, 3, 4) (3, 5, 4) |
4 個 |
| GL_TRIANGLE_FAN | 前回の三角形に使った頂点を 1 つ再利用して かつ最初の頂点は必ず再利用する |
(0, 1, 2) (0, 2, 3) (0, 3, 4) (0, 4, 5) |
4 個 |
まとめ
冒頭の四角形のポリゴンを描画するためには
- 記事中に書いた四角形用の頂点座標と頂点インデックスの配列を準備して、頂点座標を GPU へ転送しておく
- OpenGL の
glDrawElementsAPI に対して、準備した頂点インデックスと GL_TRIANGLES モードを渡して描画する
という流れになる。はい、まとめると、要するにプリミティブには
- 頂点座標
- 頂点インデックス
- 描画モード
最低限この 3 つが必要になる。たった 3 つのことだけなのにずいぶん説明が長かったけど、頂点座標と頂点インデックスはタダの配列だし、描画モードは定数になっているし、この記事の長さに比べて実際に覚えることやコーディングする量は多くはない。少しは OpenGL の Hello World に近づけた?
※ちなみに記事の途中にも書いたけど頂点インデックスは必須ではなく、描画する時に頂点インデックスの指定が必要ない glDrawArrays という API もあるけど、一般的には glDrawElements の方が柔軟だし早いとされる。
次回 バーテックスシェーダによる座標系変換 に続く。