先日、社内の勉強会でネタが募集されていたので機械学習、特にパーセプトロンについてしゃべりました。パーセプトロン自体は非常に単純なモデルで、理解も実装も比較的容易で、それゆえに様々なものの基礎になっています。近年、深層学習と呼ばれる学習を何層にも渡って行うような概念が話題になっていますが、そこに出てくるニューラルネットワークは一種の多層パーセプトロンでもあります。ここ数年での機械学習や深層学習の進歩のスピードは素晴らしいものがありますが、そんな中で基礎的な部分を押さえておくことはより大事になってくるのではないでしょうか。

社内勉強会で使ったスライドでは、簡単な機械学習の概要とパーセプトロンの仕組みを解説してみました。インターネット上に公開したので、このブログでも紹介しておきます。

補足

いくつか資料の補足をしておきたいと思います。

学習について

基本的には対象データから素性を抽出して、それを識別しながら重みが間違っていれば更新していくという流れです。素性という単語は他にも特徴量と呼ばれたりもします。スライドには、とりあえず全ての学習データが無くなるまで繰り返していくと最終的には理想的な(重みベクトルを法線とする)直線が引かれますが、そうならないこともあるのでその場合は何度か学習を繰り返します。

学習の終了判定は一定の判断基準を持って学習の終了とするか、もしくはある一定回数だけ学習を繰り返したら終了とするかのどちらかになると思います。どちらを選ぶかはケースバイケースですが、勉強や練習のためにパーセプトロンを実装するだけであれば、後者の方法の方がはるかに簡単です。

線形分離不可能について

パーセプトロンは基本的に線形分離可能な問題にしか適用することができません。それは資料のまとめの部分にも書いてある通りなのですが、あるテクニックを使うと線形分離不可能な問題にも適用することができます。

たとえば分類対象データから抽出した素性が二次元ベクトルでそれらが 2 つのクラスに分類されるんだけど、直線を引いて 2 つに分割できない、すなわち線形分離不可能な問題だった場合、その抽出された素性をより高次元な空間に写像してあげます。たとえばとある二次元の素性 (x, y) があったとすると、これを (x, y, x^2, y^2) などという四次元の空間に写像してあげて、この素性をパーセプトロンに渡して学習を繰り返すと、二次元では線形分離不可能だった問題が四次元で線形分離可能になる場合があります。

これをカーネルトリックと言います。

目に見える

スライドのタイトルにもある通り 目に見える というところが推しポイントです。何が目に見えるのかというと学習の過程です。スライドだと二次元の空間において学習していく過程を簡単に説明しました。その部分を読んだ上で今度は三次元空間において学習していく過程を表現したものを作ってみました。それがこれです。

three.js を使って作っています。まずページを開くと初期状態で以下のようなものが表示されます。各点が三次元の素性ベクトルを空間にプロットしたものです。

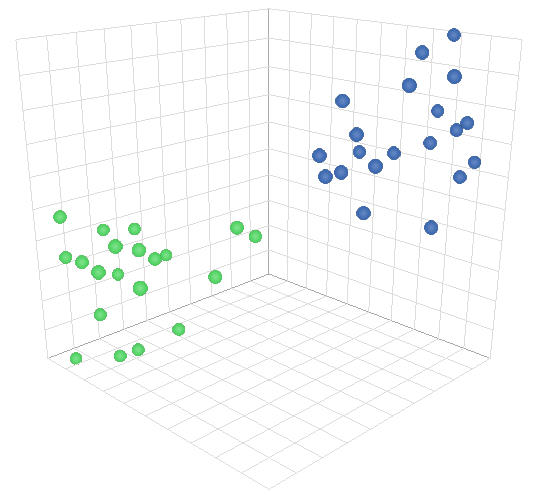
ここでスペースキーを押すたびに学習データを読み込んで学習を進めていきます。その際に都度、重みベクトル (ピンク色の矢印) を更新して空間を分割する平面 (資料では二次元なので 線 だったけど、これは三次元なので平面) が更新されていく様子がわかると思います。学習データがなくなるまで学習が進むと、青と緑の点が綺麗に 2 分割されている状態が出来上がると思います。

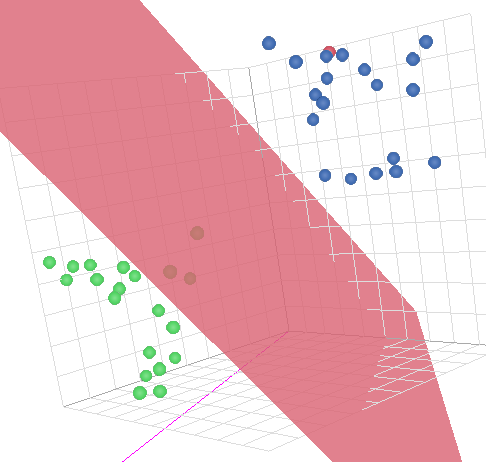
マウスでグリグリ視点を動かすことも出来るのでいろいろいじってみてください。ちなみにソースコードはこちら。

https://github.com/tkengo/perceptron_visualization

それでは。