Word2Vec というと、文字通り単語をベクトルとして表現することで単語の意味をとらえることができる手法として有名なものですが、最近だと Word2Vec を協調フィルタリングに応用する研究 (Item2Vec と呼ばれる) などもあるようで、この Word2Vec というツールは自然言語処理の分野の壁を超えて活躍しています。
実は Item2Vec を実装してみたくて Word2Vec の仕組みを理解しようとしていたのですが、Word2Vec の内部の詳細に踏み込んで解説した日本語記事を見かけることがなかったので、今更感はありますが自分の知識の整理のためにもブログに残しておきます。なお、この記事は Word2Vec のソースコードといくつかのペーパーを読んで自力で理解した内容になります。間違いが含まれている可能性もありますのでご了承ください。もし間違いを見つけた場合は指摘してもらえると修正します。
※この記事を読むにあたっては、ニューラルネットワーク及び確率的勾配降下法に関する基礎知識程度は必要です。
Word2Vec
Word2Vec の正体は、隠れ層と出力層の 2 層からなる単純なニューラルネットワークです。このニューラルネットワークに次々に単語を読み込ませて重みを学習させていくのですが、Word2Vec で獲得できる単語のベクトル表現というのは実はネットワークの重みそのものです。入力データに対する “良い表現” を獲得するという意味では自己符号化器 (オートエンコーダ) に近いものがあると思います。
Word2Vec のネットワークのアーキテクチャとしては CBoW 及び Skip-gram と呼ばれる 2 種類があり、また学習を高速化するテクニックとして Hierarchical Softmax 及び Negative Sampling の 2 種類が提案されています。Word2Vec 論文の著者が公開しているオリジナルの C のソースコードでは両方のアーキテクチャ及び高速化テクニックが実装されていますが、この記事では Skip-gram と Negative Sampling について書いていきます。CBoW 及び Hierarchical Softmax については機会があれば別途記事を書きます。
Skip-gram でモデル化する
Skip-gram とは、ある単語が与えられた時、その周辺の単語を予測するためのモデルです。たとえば以下のような単語の集合があったとしましょう。このようなものはボキャブラリと呼ばれます。
{ I, am, a, programmer, like, dog, cat }
これらの単語を使って文章を作ってください、と言われたら I am a programmer や I like a dog などの文章がすぐに思い浮かぶでしょう。ここで作った文章中の I という単語に注目すると、その次には am や like が現れて、さらにその次には a があって、それに続いて programmer や dog があります。しかし、I の次にいきなり programmer や dog といった単語はあまり現れないでしょう。つまり I という単語の周辺にはどういった単語が出現しやすいか、という確率を考えることができます。
さて、このような確率を、以下のような条件付き確率として softmax 関数を使ってモデル化します。
$$ p(w_O|w_I) = \frac{\exp(\boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I})}{\sum_{w_v \in V} \exp(\boldsymbol{v’}_{w_v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I})} $$
※$\exp(x) = \mathrm{e}^x$ です。また $\boldsymbol{v}^{\mathrm{T}}$ は $\boldsymbol{v}$ の転置、$\boldsymbol{v}^{\mathrm{T}} \cdot \boldsymbol{v}$ はベクトルの内積です。
$w_I$ は注目する単語 (添字の $I$ は Input の $I$)、$w_O$ は $w_I$ の周辺の単語 (添字の $O$ は Output の $O$)、$V$ はボキャブラリ、$\boldsymbol{v}_{w_I}$ と $\boldsymbol{v’}_{w_O}$ は単語を表すベクトルです。$\boldsymbol{v}$ と $\boldsymbol{v’}$ は別物で、$\boldsymbol{v}$ は入力ベクトル、$\boldsymbol{v’}$ は出力ベクトルと呼ばれます。さて、この式を計算することで $w_I$ と $w_O$ が共起する確率を計算できます。
たとえば $w_I$ が I であるとした時、いくつかの $w_O$ ついて例を挙げてみると
- $w_O$ が
amならば $p(am|I)$ は高くなって欲しい。I am ...は自然な文章だから。 - $w_O$ が
likeならば $p(like|I)$ は高くなって欲しい。I like ...も自然な文章だから。 - $w_O$ が
dogならば $p(dog|I)$ は低くなって欲しい。I dog ...はなんかおかしいから。
ここにコンテキスト $C$ というものを導入して、以下のような同時確率を考えます。
$$ p(w_{O,1},w_{O,2},\cdots,w_{O,C}|w_I) = \prod_{c=1}^C \frac{\exp(\boldsymbol{v’}_{w_{O,c}}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I})}{\sum_{w_v \in V} \exp(\boldsymbol{v’}_{w_v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I})} $$
ここでのコンテキスト $C$ は注目する単語の前後にある単語です。たとえば I am a programmer という文章で、前後 1 単語ずつを考える場合は以下のようになります。(このような前後の単語数をコンテキストサイズと言います。つまり以下の例ではコンテキストサイズは 1 となります)
- $w_I$ が
Iの時、$C$ は{ am } - $w_I$ が
amの時、$C$ は{ I, a } - $w_I$ が
aの時、$C$ は{ am, programmer } - $w_I$ が
programmerの時、$C$ は{ a }
このように前後のコンテキストまで含めた確率 $p(w_{O,1},w_{O,2},\cdots,w_{O,C}|w_I)$ を考えた時、その確率が最大となるようなベクトル $\boldsymbol{v}$ が、単語の “良い表現” になるであろうという仮定を置きます。それこそが Word2Vec が出力する単語ベクトルとなります。
$$ \mathop{\mathrm{argmax}}\limits_{\boldsymbol{W},\boldsymbol{W’}} p(w_{O,1},w_{O,2},\cdots,w_{O,C}|w_I) $$
※ボキャブラリの全単語に対する $\boldsymbol{v}$、$\boldsymbol{v'}$ を並べたものをそれぞれ $\boldsymbol{W}$、$\boldsymbol{W'}$ としています。
ニューラルネットワークを構築する
それでは、先ほど考えた Skip-gram のモデルに対して、以下のようなニューラルネットワークを考えます。全て全結合層になっています。$V$ はボキャブラリの単語数、$N$ は単語ベクトルの次元、$C$ はコンテキストサイズです。
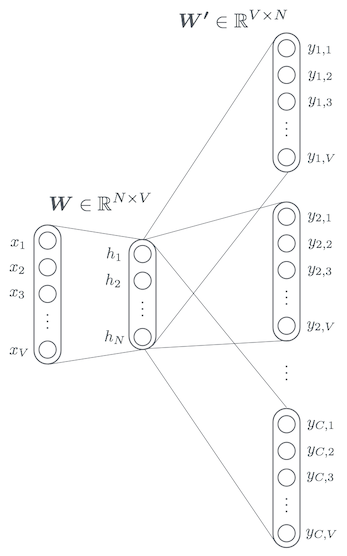
ひとつ注意ですが、これからネットワークを考えるにあたって $w_I$ や $w_O$ は実際の単語そのものではなく、ボキャブラリ内でのインデックスとして考えます。今後も最初に例として挙げた以下のようなボキャブラリを使って記事を書き進めていきますが、$w_I = 1$ だと I、$w_I = 2$ だと am、$w_I = 3$ だと a、がそれぞれ入力されたという意味になります。
{ I, am, a, programmer, like, dog, cat }
入力層
入力層のベクトル $\boldsymbol{x}$ は $V$ 次元です。ボキャブラリは一般的には $10^5$ 〜 $10^7$ 程度の語彙数になるので、$\boldsymbol{x}$ の次元もそれくらい大きなものになります。$\boldsymbol{x}$ は $w_I$ の単語に対応する要素 $x_{w_I}$ が 1 で、他はすべて 0 という、いわゆる one-hot-vector です。
たとえば $w_I = 1$ の場合、入力層のベクトル $\boldsymbol{x}$ はこのようになります。
$$
\boldsymbol{x} = \left[
\begin{array}{l}
x_1 \
x_2 \
x_3 \
x_4 \
x_5 \
x_6 \
x_7
\end{array}
\right] = \left[
\begin{array}{l}
\color{red}1 \cdots I \
0 \cdots am \
0 \cdots a \
0 \cdots programmer \
0 \cdots like \
0 \cdots dog \
0 \cdots cat
\end{array}
\right]
$$
それでは $w_I = 2$ の場合はどうでしょうか?その場合、入力層のベクトル $\boldsymbol{x}$ がこうなるのはすぐにわかるでしょう。
$$
\boldsymbol{x} = \left[
\begin{array}{l}
x_1 \
x_2 \
x_3 \
x_4 \
x_5 \
x_6 \
x_7
\end{array}
\right] = \left[
\begin{array}{l}
0 \cdots I \
\color{red}1 \cdots am \
0 \cdots a \
0 \cdots programmer \
0 \cdots like \
0 \cdots dog \
0 \cdots cat
\end{array}
\right]
$$
隠れ層
入力層から隠れ層への重み $\boldsymbol{W}$ は単語ベクトル $\boldsymbol{v}$ を並べたものです。具体的には、ボキャブラリの全単語の単語ベクトルを横に並べた行列です。$N$ 次元の単語ベクトルが $V$ 個並んだものなので行列のサイズは $N \times V$ です。ベクトルについている添字がボキャブラリの単語のインデックスに対応しています。$\boldsymbol{v}_1$ は I に対するベクトルですし、$\boldsymbol{v}_2$ は am に対するベクトルになります。
$$
\begin{eqnarray}
\boldsymbol{W} & = & \left[
\begin{array}{lllllll}
\boldsymbol{v}_1 &
\boldsymbol{v}_2 &
\boldsymbol{v}_3 &
\boldsymbol{v}_4 &
\boldsymbol{v}_5 &
\boldsymbol{v}_6 &
\boldsymbol{v}_7
\end{array}
\right] \\ & = & \left[
\begin{array}{cccc}
v_{11} & v_{21} & v_{31} & v_{41} & v_{51} & v_{61} & v_{71} \
v_{12} & v_{22} & v_{32} & v_{42} & v_{52} & v_{62} & v_{72} \
v_{13} & v_{23} & v_{33} & v_{43} & v_{53} & v_{63} & v_{73} \
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \
v_{1N} & v_{2N} & v_{3N} & v_{4N} & v_{5N} & v_{6N} & v_{7N}
\end{array}
\right]
\end{eqnarray}
$$
これが入力層から隠れ層への重み $\boldsymbol{W}$ です。隠れ層は全結合層なので、重み $\boldsymbol{W}$ と入力データ $\boldsymbol{x}$ を掛けたものが隠れ層のユニット $\boldsymbol{h}$ になります。
$$ \boldsymbol{h} = \boldsymbol{Wx} $$
さて $\boldsymbol{x}$ は one-hot-vector だったことを思い出してください。たとえば $w_I = 2$ の場合を考えてみると、以下のように結局は 2 番目の単語ベクトルがそのまま出力されることがわかります。
$$
\boldsymbol{Wx} = \left[
\begin{array}{lllllll}
\boldsymbol{v}_1 &
\boldsymbol{v}_2 &
\boldsymbol{v}_3 &
\boldsymbol{v}_4 &
\boldsymbol{v}_5 &
\boldsymbol{v}_6 &
\boldsymbol{v}_7
\end{array}
\right]\left[
\begin{array}{l}
0 \
\color{red}1 \
0 \
0 \
0 \
0 \
0
\end{array}
\right] = \boldsymbol{v}_2
$$
つまり、隠れ層のユニットは重み行列の $w_I$ 列目の単語ベクトルそのものとなることがわかります。このネットワークでは隠れ層に活性化関数は使いませんので、隠れ層の出力はそのまま $\boldsymbol{v}_{w_I}$ となります。
$$ \boldsymbol{h} = \boldsymbol{Wx}_{w_I} = \boldsymbol{v}_{w_I} $$
出力層
隠れ層から出力層への重み $\boldsymbol{W’}$ も同じように単語ベクトル $\boldsymbol{v’}$ を並べたものです。$\boldsymbol{W}$ と同じように、ボキャブラリの全単語の単語ベクトルを並べます。ただし今度は各単語ベクトルを転置したものを縦に並べた行列です。こちらは $V \times N$ のサイズになります。
$$
\boldsymbol{W’} = \left[
\begin{array}{l}
\boldsymbol{v’}_1^{\mathrm{T}} \
\boldsymbol{v’}_2^{\mathrm{T}} \
\boldsymbol{v’}_3^{\mathrm{T}} \
\boldsymbol{v’}_4^{\mathrm{T}} \
\boldsymbol{v’}_5^{\mathrm{T}} \
\boldsymbol{v’}_6^{\mathrm{T}} \
\boldsymbol{v’}_7^{\mathrm{T}}
\end{array}
\right] = \left[
\begin{array}{ccccc}
v’_{11} & v’_{12} & v’_{13} & \cdots & v’_{1N} \
v’_{21} & v’_{22} & v’_{23} & \cdots & v’_{2N} \
v’_{31} & v’_{32} & v’_{33} & \cdots & v’_{3N} \
v’_{41} & v’_{42} & v’_{43} & \cdots & v’_{4N} \
v’_{51} & v’_{52} & v’_{53} & \cdots & v’_{5N} \
v’_{61} & v’_{62} & v’_{63} & \cdots & v’_{6N} \
v’_{71} & v’_{72} & v’_{73} & \cdots & v’_{7N}
\end{array}
\right]
$$
出力層にはコンテキストサイズ $C$ の分だけユニットがあり、各コンテキストでは重み $\boldsymbol{W’}$ を共有します。出力層も各コンテキスト毎に全結合されているので、重み $\boldsymbol{W’}$ と隠れ層の出力値 $\boldsymbol{v}_{w_I}$ を掛けたものが、出力層の各コンテキストのユニット $\boldsymbol{u}_c$ になります。
$$ \boldsymbol{u}_c = \boldsymbol{W’v}_{w_I} $$
出力層での活性化関数は softmax 関数を使いますので、最終的な出力値 $y_{c,i}$ は以下のようになります。この $y_{c,i}$ は、最初に Skip-gram でモデル化した時の確率になることは既にお分かりでしょう。
$$ y_{c,i} = \frac{\exp(u_{c,i})}{\sum_{v=1}^V \exp(u_{c,v})} = \frac{\exp(\boldsymbol{v’}_i \cdot \boldsymbol{v}_{w_I})}{\sum_{v=1}^V \exp(\boldsymbol{v’}_v \cdot \boldsymbol{v}_{w_I})} = p(w_{i}|w_I) $$
最適なパラメータを見つける
ネットワークの全貌が把握できたところで、重みを最適化する作業に入っていきましょう。ニューラルネットワークの最適化で最も良く使われるのは確率的勾配降下法 (SGD) ですので、ここでも SGD を使って最適化していきます。目標としているのは $w_I$ の周辺コンテキストにおいて各単語の出現確率を考えた同時確率 $p(w_1,w_2,\cdots,w_C|w_I)$ を最大化するような単語のベクトル表現を見つけることです。
SGD の目的関数として、以下のものを使います。
$$ E = - \log p(w_1,w_2,\cdots,w_C|w_I) \tag{1} $$
※ここでの対数は自然対数です。つまり底は $\mathrm{e}$ です。
先頭にマイナスをつけたのは、最大化問題を最小化問題に置き換えるためです。$f(x)$ を最大化する問題と、$-f(x)$ を最小化する問題は同じだということですね。
また、対数をとったのはアンダーフローを防ぎつつ計算を楽にするためです。今回、最適化の対象となる関数は前述の通り同時確率であり、同時確率の計算は 1 以下の数字を何度もかけることになりますので、値がどんどん小さくなっていきます。対数をとると、掛け算を足し算に変換できますので値が小さくなることを防げると共により簡単な足し算として計算できるようになります。
では、今考えているネットワークに対応させるために (1) を、ネットワークの出力 $y$ を使って表します。$p(w_1,w_2,\cdots,w_C|w_I)$ は、最初の方にも出てきましたが softmax の掛け算なので $y$ を使って以下のように表すことができます。
$$ p(w_1,w_2,\cdots,w_C|w_I) = \prod_{c=1}^C y_{c,w_c} \tag{2} $$
この (2) を (1) に代入して変形を繰り返していくと、最終的には目的関数は以下のような形になります。
$$ E = - \sum_{c=1}^C \left( u_{c,w_c} - \log \sum_{v=1}^V \exp(u_{c,v}) \right) \tag{3} $$
最小化すべき目的関数 $E$ がわかったところで、$E$ を出力層と隠れ層の重み $\boldsymbol{W’}, \boldsymbol{W}$ の各要素で偏微分し、以下のような重みの更新式を得ることができます。
$$
\begin{eqnarray}
v’_{ij} & := & v’_{ij} - \eta \sum_{c=1}^C (y_{c,i} - t_{c,i}) v_{w_Ij} \
v_{w_Ii} & := & v_{w_Ii} - \eta \sum_{c=1}^C \sum_{v=1}^V (y_{c,v} - t_{c,v}) v’_{vi}
\end{eqnarray}
$$
※目的関数の変形及び偏微分の計算は省略しているので、興味のある人は補填を参照。
目的関数の導出, $v'_{ij}$ での偏微分, $v_{w_I}$ での偏微分
Negative Sampling
ニューラルネットワークを構築し、重みの更新式も手に入れたのであとは実装するのみになりました。さて、実装できたので学習するぞー、と意気込んで学習を始めてみたところ 1 つの問題にぶち当たります。それは計算量が爆発しすぎて学習がなかなか終わらない問題です。ネットワークの出力値である $y_{c,i}$ について思い出してみてください。
$$ y_{c,i} = \frac{\exp(\boldsymbol{v’}_i \cdot \boldsymbol{v}_{w_I})}{\sum_{v=1}^V \exp(\boldsymbol{v’}_v \cdot \boldsymbol{v}_{w_I})} $$
この式の分母に $V$ 回の繰り返しがあります。これまで使用してきたサンプルボキャブラリでは 7 個しか単語がなかったため問題ありませんが、先にも書いたように一般的に $V$ の語彙数は $10^5$ 〜 $10^7$ オーダーであるため、この部分の計算コストが高くつきます。しかもこれは、学習のイテレーション毎に計算しなおさなければなりませんので、なかなか学習が終わりません。そこで使われる高速化のテクニックが Negative Sampling です。
ある単語のペア $(w_I, w_O)$ が学習データから生成されたかどうかの確率を考え、それを $p(D=1|w_I,w_O)$ として、また逆に学習データから生成されて “いない” 確率を $p(D=0|w_I,w_O)$ とします。$D=1$ の方はシグモイド関数とし、$D=0$ の方は確率の定義から以下のようになります。
$$
\begin{eqnarray}
p(D=1|w_I,w_O) & = & \sigma(\boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) \
p(D=0|w_I,w_O) & = & 1 - p(D=1|w_I,w_O)
\end{eqnarray}
$$
上の 2 式から以下のような新しい目的関数を考えます。
$$ E = - \log p(D=1|w_I,w_O) \prod_{v \in V_{Neg}} p(D=0|w_I,v) \tag{4} $$
新しく $V_{Neg}$ という集合が出てきましたが、これは元々のボキャブラリの集合から適当に $k$ 個だけサンプリングしてきたものです。この $k$ 個のサンプルはランダムに選ばれるわけではなく、とある $P_n(w)$ という確率分布から生成されるサンプルを集めます。この $P_n(w)$ をノイズ分布と言い、Word2Vec では以下の様な確率分布をノイズ分布 $P_n(w)$ として使っています。式中の $U(w)$ は学習データ中に単語 $w$ が出現する回数です。
$$ P_n(w) = \frac{U(w)^{\frac{3}{4}}}{\sum_{v=1}^V U(w_v)^{\frac{3}{4}}} $$
このように学習に $k$ 個程度のサンプルを不正解データとして混ぜ込むことから Negative Sampling という名前がついています。この $k$ という値は、論文によると通常 5 〜 20 程度で十分であり、またデータセットが十分に大きければ 2 〜 5 個程度でも良い性能を発揮してくれるとのことです。
(4) の目的関数を最小化することで、正解単語には高い確率が割り当てられ、不正解単語 (ノイズ) には低い確率が割り当てられるような動きになり、それを元に単語ベクトルが学習されていきますが、この目的関数の意味するところは本質的には softmax 関数の近似です。元々は softmax の式を求めるためには $V$ 回の繰り返し計算が不可欠でしたが、これはたかだか $k+1$ 回の計算で softmax を近似できているため計算量的にかなり楽になっています。Noise Contrastive Estimation (NCE) と呼ばれる手法で別途論文が書かれており、それを参考にしているようです。
さて、(4) の目的関数を変形していくと最終的に以下のような式が得られます。
$$ E = - \log \sigma(\boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - \sum_{v \in V_{Neg}} \log \sigma(-\boldsymbol{v’}_{v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) $$
Skip-gram でやったのと同じように重みの更新式を導出するために $E$ を偏微分すると、最終的には以下のような重みの更新式が得られます。
$$
\begin{eqnarray}
v’_{ij} & := & v’_{ij} - \eta (\sigma(\boldsymbol{v’}_i^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - t_i) v_{w_Ij} \
v_{w_Ii} & := & v_{w_Ii} - \eta \sum_{v \in \{w_O\} \cup V_{Neg}} (\sigma(\boldsymbol{v’}_{v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - t_{v}) v’_{vi}
\end{eqnarray}
$$
※目的関数の変形及び偏微分の計算は省略しているので、興味のある人は補填を参照。
目的関数の導出, $v'_{ij}$ での偏微分, $v_{w_I}$ での偏微分
まとめ
Word2Vec の内部構造について書いてみました。中身がわからないうちはどうやって動いているんだろうと不思議でしたが、ちゃんと調べてみると自分でも理解できるような単純なニューラルネットワークだったので意外でした。結局やっているのは単純な 2 層ネットワークの重みの最適化ですしね。Negative Sampling の紹介もしましたが、こちらは高速化テクニックになるので不要であれば必ず実装する必要はありません。実際 Negative Sampling は Skip-gram が発表されてからしばらく後に提案されたもののようですし、時間がかかりながらも頑張って (3) の目的関数を最適化すればうまくいくのでしょう (やったことないけど)。
もしこれを読んでおおまかな流れがわかったのであれば、Word2Vec のソースコードを読む、または自分で実装してみるのも面白いと思います。私が読んだことがあるのはオリジナルの C での実装だけですが、世の中には他にも Python (gensim) や Java (Deepleaning4j) での実装があり、また Chainer や TensorFlow などのフレームワークを使った実装もあるようなので、学習環境には事欠かないのではないでしょうか。
最後に面白かったのが、とある論文の最後に「なぜこれが良い単語表現を見つけてくれるのか」という章があり、その内容が「良い質問だ。我々もまったく知らない」だったことです。ニューラルネットワーク界隈は経験則的にそれが良い結果を生み出すことはわかっていても、理論的になぜそうなるのかはわかっていないような問題が多く、Word2Vec もその典型なのでしょう。
参考リンク
論文集
- Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean. Efficient Estimation of Word Representations in Vector Space. 2013
- Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, Jeffrey Dean. Distributed Representations of Words and Phrases and their Compositionality. 2013
- Yoav Goldberg, Omer Levy. word2vec Explained: deriving Mikolov et al.’s negative-sampling word-embedding method. 2014
- Xin Rong. word2vec Parameter Learning Explained. 2014
実装
補填
本記事中で式の導出について省略した部分を、途中の式を示しながら導出していきます。
Skip-gram の目的関数
(2) を (1) に代入すると Skip-gram の目的関数は以下の形をしています。
$$
\begin{eqnarray}
E & = & - \log \prod_{c=1}^C y_{c,w_c} \
& = & - \log \prod_{c=1}^C \frac{\exp(u_{c,w_c})}{\sum_{v=1}^V \exp(u_{c,v})}
\end{eqnarray}
$$
$\log$ の中身を掛け算から足し算に変換できる $\log(a \cdot b) = \log a + \log b$ という性質を利用すると、掛け算 $\prod$ は全部足し算 $\sum$ に変換できます。
$$ E = - \sum_{c=1}^C \log \frac{\exp(u_{c,w_c})}{\sum_{v=1}^V \exp(u_{c,v})} $$
今度は $\log$ の中身を割り算から引き算に変換できる $\log \frac{a}{b} = \log a - \log b$ という性質を利用すると、softmax 関数の部分を以下のように変換できます。
$$ E = - \sum_{c=1}^C \left( \log \exp(u_{c,w_c}) - \log \sum_{v=1}^V \exp(u_{c,v}) \right) $$
$\log \exp(x) = x$ なので、第一項の $\log \exp$ の部分がなくなります。
$$ E = - \sum_{c=1}^C \left( u_{c,w_c} - \log \sum_{v=1}^V \exp(u_{c,v}) \right) $$
これで (3) が導出できました。
Skip-gram の重み更新 (出力層)
出力層の重み $\boldsymbol{W’}$ の各要素で $E$ を偏微分するので以下を求めることになります。
$$ \frac{\partial E}{\partial v’_{ij}} $$
このままだと少しイメージし難いのでまず 1 つ具体的に、たとえば $v’_{11}$ で偏微分することを考えてみます。$v’_{11}$ は $\boldsymbol{W’}$ の 1 行目 1 列目の要素です。これが目的関数 $E$ の中のどこに出てくるかというと、出力層の各コンテキストのユニット $\boldsymbol{u}_c$ の 1 つ目の要素に含まれることになります。$\boldsymbol{u}_c$ の定義は以下のようなベクトルでした。
$$
\boldsymbol{u}_c= \boldsymbol{W’v}_{w_I} = \left[
\begin{array}{c}
u_{c,1} \
u_{c,2} \
\vdots \
u_{c,7}
\end{array}
\right] = \left[
\begin{array}{c}
\color{red}v’_{11}v_{w_I1}\color{black} + v’_{12}v_{w_I2} + \cdots + v’_{1N}v_{w_IN} \
v’_{21}v_{w_I1} + v’_{22}v_{w_I2} + \cdots + v’_{2N}v_{w_IN} \
\vdots \
v’_{71}v_{w_I1} + v’_{72}v_{w_I2} + \cdots + v’_{7N}v_{w_IN} \
\end{array}
\right] \tag{5}
$$
これを一般化すると $v’_{ij}$ は $\boldsymbol{u}_c$ の $i$ 番目の要素 $u_{c,i}$ に含まれていると言えます。コンテキストは $C$ 個あるので偏微分は連鎖率を使って次のように分割できます。
$$ \frac{\partial E}{\partial v’_{ij}} = \sum_{c=1}^C \frac{\partial E}{\partial u_{c,i}} \frac{\partial u_{c,i}}{\partial v’_{ij}} \tag{6} $$
これをさらに計算していきます。項が 2 つあるので、まず最初に第一項、つまり $E$ を $u_{c,i}$ で偏微分するところから計算していきます。(3) の $E$ の $\sum$ を展開して以下のようにします。
$$
\begin{eqnarray}
E & = & - \sum_{c’=1}^C \left( u_{c’,w_{c’}} - \log \sum_{v=1}^V \exp(u_{c’,v}) \right) \
& = & - \sum_{c’=1}^C u_{c’,w_{c’}} + \sum_{c’=1}^C \log \sum_{v=1}^V \exp(u_{c’,v})
\end{eqnarray}
$$
※$C$ に対する $\sum$ の変数が $c'$ になっているのは、既に (6) で $c$ を使っており、それとは区別したいためです。
これを $u_{c,i}$ で微分することを考えるのですが、さらにまた 第一項と第二項で分けて考えます。はじめに第一項についてですが、わかりやすくするために $\sum$ をはずしてみます。
$$ \sum_{c’=1}^C u_{c’,w_{c’}} = u_{1,w_1} + u_{2,w_2} + \cdots + u_{C,w_C} $$
たとえば偏微分する変数が $u_{1,i}$ だとすると $i = w_1$ であれば $u_{1,w_1}$ が微分されて 1 になるのがわかります。$u_{2,i}$ の場合も同じですね、$i = w_2$ であれば $u_{2,w_2}$ が微分されて結果は 1 になります。一般的に述べると偏微分する変数が $u_{c,i}$ の場合、$i = w_c$ であれば 1、それ以外であれば 0 ということになります。場合分けが入ると面倒なのでこれを $t_{c,i}$ という文字で表します。
$$
t_{c,i} = \begin{cases}
1 & (i = w_c) \
0 & (otherwise)
\end{cases}
$$
さらに第二項については、以下のように置き換えて連鎖率を使って微分します。
$$
\begin{eqnarray}
g & = & \sum_{v=1}^V \exp(u_{c,v}) \
f & = & \log g \
\
\frac{df}{dg} \frac{dg}{du_{c,i}} & = & \frac{1}{g} \exp(u_{c,i}) = \frac{\exp(u_{c,i})}{\sum_{v=1}^V \exp(u_{c,v})} = y_{c,i}
\end{eqnarray}
$$
これでようやく (6) の第一項が求まったことになり、最終的には以下のような形になります。
$$ \frac{\partial E}{\partial u_{c,i}} = y_{c,i} - t_{c,i} \tag{7} $$
また、(6) の第二項は
$$ u_{c,i} = v’_{i1} v_{w_I1} + v’_{i2} v_{w_I2} + \cdots + \color{red} v’_{ij} v_{w_Ij} \color{black} + \cdots + v’_{iN} v_{w_IN} $$
となるので、以下のように簡単に求められます。
$$ \frac{\partial u_{c,i}}{\partial v’_{ij}} = v_{w_Ij} \tag{8} $$
(6) (7) (8) を合わせると最終的に出力層の重みでの偏微分の結果が得られます。
$$ \frac{\partial E}{\partial v’_{ij}} = \sum_{c=1}^C (y_{c,i} - t_{c,i}) v_{w_Ij} $$
Skip-gram の重み更新 (隠れ層)
同じようにして今度は隠れ層の重み $\boldsymbol{W}$ の更新を考えていきます。ただし $\boldsymbol{W}$ は $\boldsymbol{W’}$ と違って、1 回の更新ですべての要素 $v_{ij}$ を更新することができません。どういうことかというと、今考えているニューラルネットワークでは $\boldsymbol{v}_{w_I}$ の重みしか伝搬していかないからです。
たとえば $w_I = 1$ の時を考えてみます。入力層のベクトル $\boldsymbol{x}$ は one-hot-vector だったために、隠れ層のユニットは $\boldsymbol{v}_1$ になるということを思い出してください。すると、その後の $\boldsymbol{u}_c$ や $\boldsymbol{y}_c$ には $\boldsymbol{v}_1$ の重みしか含まれておらず、他の $\boldsymbol{v}_2, \boldsymbol{v}_3, \cdots, \boldsymbol{v}_7$ は出てきません。このような状態で $\boldsymbol{v}_1$ 以外で偏微分したとしても全て 0 になってしまうので重みの更新ができません。
結局、ネットワークの入力となる $w_I$ に対応する重み $\boldsymbol{v}_{w_I}$ のみが更新できて、他は計算するだけ無駄になるため、ここでは $\boldsymbol{v}_{w_I}$ で偏微分することだけを考えます。出力層の重みを求めた時と同じように目的関数 $E$ のどこに $v_{w_Ii}$ が出てくるのかを探してみます。(5) を見てみると $v_{w_Ii}$ は $\boldsymbol{u}_c$ のどの要素にも含まれているのがわかります。$\boldsymbol{u}_c$ の要素数は $V$ 個、そしてコンテキストは $C$ 個あって、その全てに $v_{w_Ii}$ が含まれているので、偏微分は以下のようになります。
$$ \frac{\partial E}{\partial v_{w_Ii}} = \sum_{c=1}^C \sum_{v=1}^V \frac{\partial E}{\partial u_{c,v}} \frac{\partial u_{c,v}}{\partial v_{w_Ii}} \tag{9} $$
項が 2 つあるのでこちらもそれぞれで計算していくのですが、第一項は既に (7) で求めているので計算の必要はありません。また、第二項の方は (5) を見れば
$$ u_{c,v} = v’_{v1} v_{w_I1} + v’_{v2} v_{w_I2} + \cdots + \color{red} v’_{vi} v_{w_Ii} \color{black} + \cdots + v’_{vN} v_{w_IN} $$
となるので、以下のように簡単に求められます。
$$ \frac{\partial u_{c,v}}{\partial v_{w_Ii}} = v’_{vi} \tag{10} $$
(9) (7) (10) を合わせると最終的に隠れ層の重みでの偏微分の結果が得られます。
$$ \frac{\partial E}{\partial v_{w_Ii}} = \sum_{c=1}^C \sum_{v=1}^V (y_{c,v} - t_{c,v}) v’_{vi} $$
Negative Sampling の目的関数
以下の Negative Sampling の目的関数の最終的な形を導出していきます。
$$ E = - \log p(D=1|w_I,w_O) \prod_{v \in V_{Neg}} p(D=0|w_I,v) $$
まず $D=1$ の場合と $D=0$ の場合を、それぞれシグモイド関数 $\sigma$ を使って表せるので、それを求めてみます。$D=1$ の場合は 定義 より $\sigma$ そのものなのでこれはよいでしょう。$D=0$ の場合は以下のように計算して求めることができます。表記の簡単のために $u = \boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}$ と置いて計算を進めてみます。
$$
\begin{eqnarray}
p(D=0|w_I,w_O) & = & 1 - p(D=1|w_I,w_O) \
& = & 1 - \sigma(u) \
& = & 1 - \frac{1}{1 + \exp(-u)} \
& = & \frac{\exp(-u)}{1 + \exp(-u)} \
& = & \frac{1}{(1 + \exp(-u))\exp(u)} \
& = & \frac{1}{1 + \exp(u)} \
& = & \sigma(-u)
\end{eqnarray}
$$
3, 4 行目は通分しており、4,5 行目は $\exp(-u) = \frac{1}{\exp(u)}$ を使いました。つまり目的関数 $E$ は $\sigma$ を使って以下のように書き直せます。
$$ E = - \log \sigma(\boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) \prod_{v \in V_{Neg}} \sigma(-\boldsymbol{v’}_{v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) $$
あとは Skip-gram の時と同じように $\log$ の中身を掛け算から足し算に変換できる $\log(a \cdot b) = \log a + \log b$ という性質を利用して、最終的な形に持っていくことができます。
$$ E = - \log \sigma(\boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - \sum_{v \in V_{Neg}} \log \sigma(-\boldsymbol{v’}_{v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) $$
Negative Sampling の重み更新 (出力層)
出力層の重み $\boldsymbol{W′}$ の各要素で $E$ を偏微分するので以下を求めることになります。
$$ \frac{\partial E}{\partial v’_{ij}} $$
前提として、Skip-gram と違って 1 回の更新で $\boldsymbol{W’}$ の全ての要素 $v_{ij}$ を更新することはできません。なぜなら目的関数 $E$ には $w_O$ 及び $v \in V_{Neg}$ の単語に対応する単語ベクトル $\boldsymbol{v’}$ しか含まれていないため、その他の要素での偏微分は全て 0 になり、そのような要素については重みの更新はできないからです。という注意書きをしておいて、それでは計算に進みます。
さて、目的関数 $E$ を以下のように置き換えて、連鎖率を使って微分するようにしてみます。
$$
\begin{eqnarray}
u_k & = & \boldsymbol{v’}_k^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I} \
E & = & - \log \sigma(u_{w_O}) - \sum_{v \in V_{Neg}} \log \sigma(-u_{v}) \
\frac{\partial E}{\partial v’_{ij}} & = & \frac{\partial E}{\partial u_i} \frac{\partial u_i}{\partial v’_{ij}} \tag{11}
\end{eqnarray}
$$
まずは (11) の第一項から、つまり $E$ を $u_i$ で偏微分するところから考えてみます。これは $u_i$ の $i$ が $w_O$ なのか、それ以外なのかで微分結果が変わってくるため場合分けをします。まず $i = w_O$ の場合、$u_i$ は $E$ の第一項にだけ含まれているので、その部分を以下のように連鎖率を使って微分します。
$$
\begin{eqnarray}
f & = & \sigma(u_i) \
E & = & - \log f - \sum_{v \in V_{Neg}} \log \sigma(-u_{v}) \
\frac{\partial E}{\partial f} \frac{\partial f}{\partial u_i} & = & - \frac{1}{f} \sigma’(u_i) \
& = & - \frac{(1 - \sigma(u_i))\sigma(u_i)}{\sigma(u_i)} \
& = & \sigma(u_i) - 1 \tag{12}
\end{eqnarray}
$$
※$\sigma'(x) = (1 - \sigma(x))\sigma(x)$ という式を利用しています。
次に $i \in V_{Neg}$ の場合について、こちらもまた連鎖率を使って以下のように微分していきます。
$$
\begin{eqnarray}
f_i & = & \sigma(-u_i) \
E & = & - \log \sigma(u_{w_O}) - \sum_{v \in V_{Neg}} \log f_{v} \
\frac{\partial E}{\partial f_i} \frac{\partial f_i}{\partial u_i} & = & - \frac{1}{f_i} \sigma’(-u_i) \
& = & \frac{(1 - \sigma(-u_i))\sigma(-u_i)}{\sigma(-u_i)} \
& = & 1 - (1 - \sigma(u_i)) \
& = & \sigma(u_i) \tag{13}
\end{eqnarray}
$$
※$\sigma'(-x) = -(1 - \sigma(-x))\sigma(-x)$ と $\sigma(-x) = 1 - \sigma(x)$ という式を利用しています。
(12) と (13) を見比べると -1 がついているかいないかの違いしかないので、場合分けについて $t_i$ という変数を用意して隠すと、結局 $E$ を $u_i$ で偏微分した結果は以下のようになります。
$$
t_i = \begin{cases}
1 & (i = w_O) \
0 & (otherwise)
\end{cases}
$$
$$ \frac{\partial E}{\partial u_i} = \sigma(u_i) - t_i \tag{14} $$
ここまで来るとあとは (11) の第二項を求めれば良いだけですが、これは
$$ u_i = v’_{i1} v_{w_I1} + v’_{i2} v_{w_I2} + \cdots + \color{red} v’_{ij} v_{w_Ij} \color{black} + \cdots + v’_{w_iN} v_{w_IN} $$
なので、以下のように簡単に求められます。
$$ \frac{\partial u_i}{\partial v’_{ij}} = v_{w_Ij} $$
ということで、出力層の重み $\boldsymbol{W’}$ の各要素での偏微分結果については以下のような式が得られます。
$$ \frac{\partial E}{\partial v’_{ij}} = (\sigma(\boldsymbol{v’}_i^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - t_i) v_{w_Ij} $$
Negative Sampling の重み更新 (隠れ層)
隠れ層の重み $\boldsymbol{W}$ の各要素での偏微分を見ていきます。Skip-gram の時と同じように $\boldsymbol{W}$ については $\boldsymbol{v}_{w_I}$ の重みしか伝搬しないため $v_{w_Ii}$ の偏微分のみ計算すれば十分です。まず始めに $\boldsymbol{v}_{w_I}$ が $E$ の中のどこに含まれているかを探してみます。
$$ E = - \log \sigma(\boldsymbol{v’}_{w_O}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - \sum_{v \in V_{Neg}} \log \sigma(-\boldsymbol{v’}_{v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) $$
これを見て分かる通り $\boldsymbol{v}_{w_I}$ は全ての項に含まれていることがわかるので、連鎖率を使うと以下のように表すことができます。
$$
\begin{eqnarray}
u_k & = & \boldsymbol{v’}_k^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I} \
E & = & - \log \sigma(u_{w_O}) - \sum_{v \in V_{Neg}} \log \sigma(-u_{v}) \
\frac{\partial E}{\partial v_{w_Ii}} & = & \sum_{v \in \{w_O\} \cup V_{Neg}} \frac{\partial E}{\partial u_{v}} \frac{\partial u_{v}}{\partial v_{w_Ij}}
\end{eqnarray}
$$
これの第一項については既に (14) で求めているため計算する必要はありません。そして第二項については
$$ u_{v} = v’_{v1} v_{w_I1} + v’_{v2} v_{w_I2} + \cdots + \color{red} v’_{vi} v_{w_Ii} \color{black} + \cdots + v’_{vN} v_{w_IN} $$
なので、以下のように簡単に求められます。
$$ \frac{\partial u_{v}}{\partial v_{w_Ii}} = v’_{vi} $$
よって偏微分は以下のようになります。
$$ \frac{\partial E}{\partial v_{w_Ii}} = \sum_{v \in \{w_O\} \cup V_{Neg}} (\sigma(\boldsymbol{v’}_{v}^{\mathrm{T}} \cdot \boldsymbol{v}_{w_I}) - t_{v}) v’_{vi} $$